COMPUTAÇÃO NA ESCOLA
Sistemas de Numeração
Para um ilustre homem das cavernas, o número 8 era representado através de 8 traços verticais (IIIIIIII), ao passo que, para um soldado romano, o número 8 era escrito como “VIII”. Um sistema de numeração consiste precisamente num conjunto de símbolos e regras que permitem representar números de uma forma consistente. Como serão então representados os números num computador? 🤔
ENSICO(Texto)
É uma grande coincidência o voo 666 da companhia aérea Finnair ter aterrado em HEL (Helsínquia) numa sexta-feira 13. Mas não é uma coincidência o facto de termos 10 dedos nas mãos e utilizarmos 10 algarismos para representar os números. E, se o ser humano possuísse apenas 2 dedos no total, talvez estivesse mais próximo de um computador do que possamos imaginar.
História e Curiosidades
Ao longo da História, diferentes civilizações representaram os números que conhecemos de diferentes formas. Por exemplo, para um ilustre homem das cavernas, o número 8 era representado através de 8 traços verticais (IIIIIIII), ao passo que, para um soldado romano, o número 8 era escrito como “VIII”.

Um sistema de numeração consiste precisamente num conjunto de símbolos e regras que permitem representar números de uma forma consistente. Atualmente, nós utilizamos o chamado sistema hindu-arábico, inventado por matemáticos indianos há bué tempo atrás (entre os séculos I e IV).

Neste sistema, existem 10 algarismos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) que, quando escritos lado a lado, permitem representar os números que tão bem conhecemos e utilizamos, como o 273 ou o número de telemóvel do Cristiano Ronaldo.

Este sistema é bastante conveniente para o ser humano, uma vez que possuímos um total de 10 dedos nas mãos, o que facilita o ato de contar. É por este motivo que também costumamos relacionar grandezas através de potências de 10: um metro são 100 centímetros; um quilograma são 1000 gramas, etc.
Mas, espera lá... Se assim é, por que motivo uma hora são 60 minutos e um minuto são 60 segundos? 🤔 Parece que, nesta matéria, a “culpa” é dos antigos babilónios. De facto, ao invés de 10 símbolos, eles utilizavam 60 símbolos diferentes para representar os números! Logo, estavam habituados a relacionar grandezas através de potências e múltiplos de 60. É também por este motivo que consideramos que uma volta completa tem uma amplitude de 360º – o número 360 é precisamente 60 × 6.
A loucura total ocorre em certas regiões de Papua-Nova Guiné, em que alguns habitantes falam uma língua chamada bukiyip. De facto, são aqui utilizados simultaneamente dois sistemas de numeração distintos. É empregue um sistema baseado em 3 símbolos para contar dias, cocos, peixes, entre outros; e um sistema baseado em 4 símbolos para representar quantidades relativas a nozes, bananas e escudos, por exemplo. Assim, a palavra anauwip, consoante o contexto, pode referir-se a 6 dias ou 24 bananas 😜

OK, por esta altura, já deves estar a pensar: o que tem isto a ver com computação?! Essa é uma questão deveras pertinente, e é precisamente disso que agora vamos falar 😉
Sistema Binário
Como já deves estar farto de saber, os computadores funcionam à base de 0s e 1s, os chamados bits. Todas as maravilhas que fazem acabam por se resumir a estes dois singelos símbolos. Em particular, qualquer tipo de informação – incluindo números – é representada através de sequências de 0s e 1s. Logo, podemos mesmo dizer que o sistema de numeração mais importante em computação é o sistema binário.
A questão que agora colocamos é a seguinte: como decifrar o número a que corresponde a sequência de bits 10110, por exemplo? Será o 7? Será o 24? Será o número de telemóvel do Cristiano Ronaldo? 🙄

Assim como, no nosso sistema baseado em 10 algarismos, as potências de 10 (como 1, 10, 100, 1000, 10000...) desempenham um papel importante, no sistema binário são as potências de 2 (1, 2, 4, 8, 16, 32...) que merecem o estrelato. Repara que estes valores são obtidos partindo do número 1 e multiplicando sucessivamente por 2:
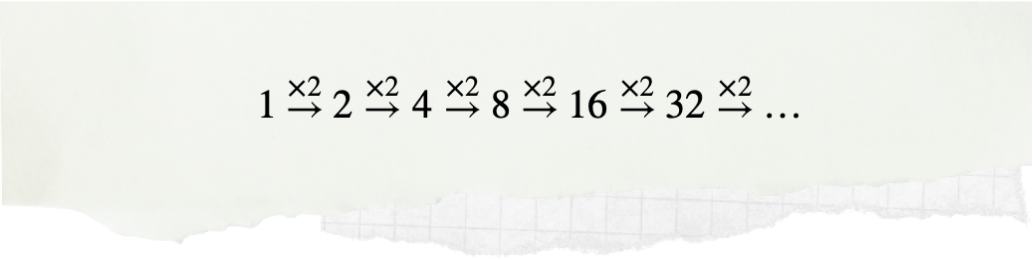
Deste modo, para decifrarmos o número decimal (ou seja, o “nosso” número) que é representado pelo número binário 10110, começamos por escrever a sequência das potências de dois – 1, 2, 4, 8... – da direita para a esquerda, por baixo de cada bit:

Depois, multiplicamos os dois valores de cada coluna e calculamos o resultado:

Para terminar, somamos todos estes produtos, obtendo 16 + 0 + 4 + 2 + 0 = 22. Deste modo, o número binário 10110 representa o “nosso” 22.
Este mesmo raciocínio pode também ser aplicado usando as nossas conhecidas “árvores binárias” (recorda o artigo 3Bs: Bits, Bytes e Basic). Basta colocar, partindo da base inferior da árvore, cada uma dessas potências de 2 em cada nível da árvore binária, como ilustrado na figura abaixo. Depois é só percorrer cada “caminho” somando os números associados ao bit 1, obtendo desse modo o número decimal que representa um determinado código binário e vice-versa. Por exemplo, olhando para a árvore abaixo, o número binário 01111 representa o “nosso” 15, uma vez que 15 = 8 + 4 + 2 + 1; e, simultaneamente, o “nosso” 15 é representado pelo número binário 01111.
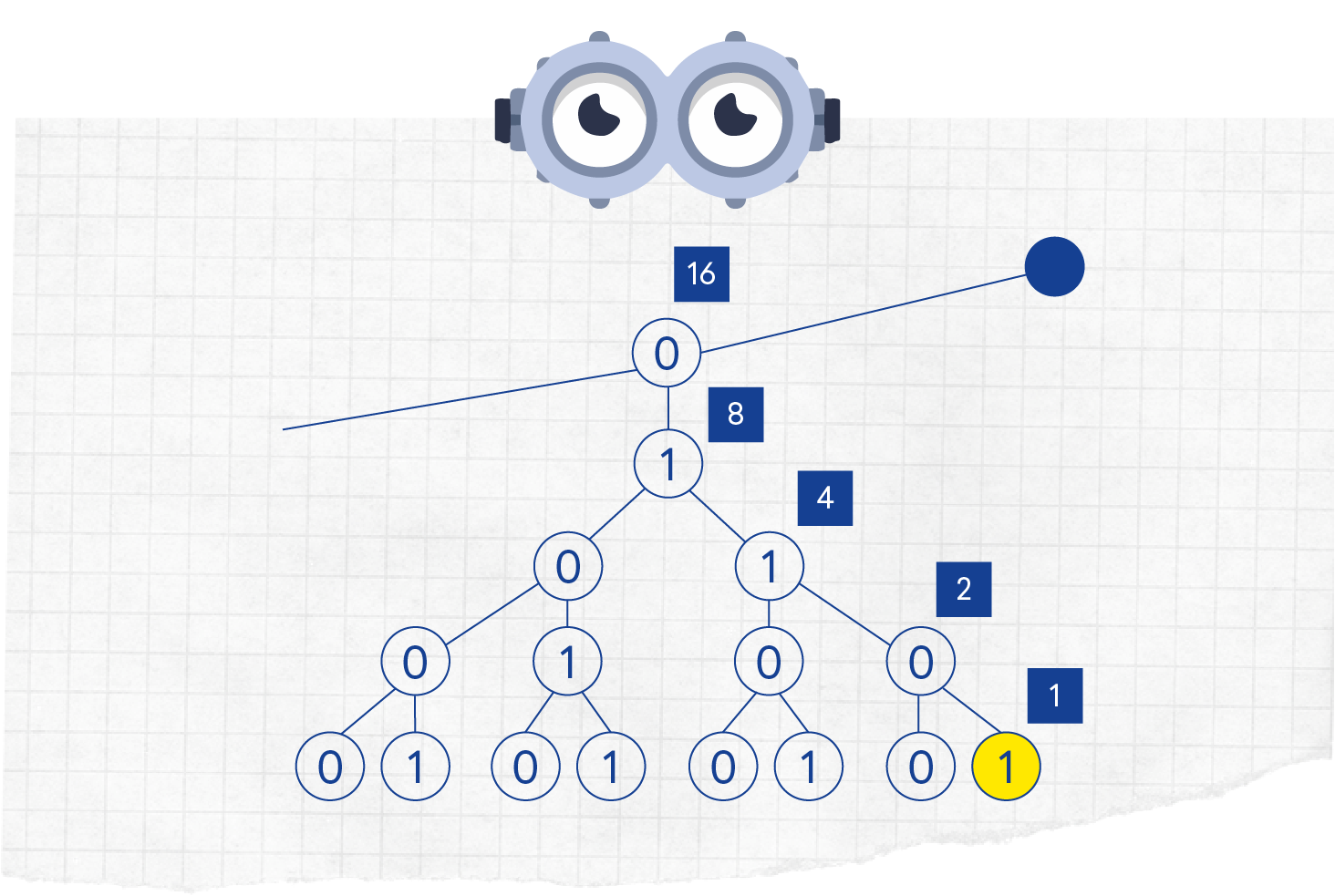
Entendido? Vamos então pôr à prova as tuas skills de conversão nos próximos desafios! 😎
DESAFIO
Descobre quais os números que estão a ser representados por cada uma das sequências de bits seguintes:

Embora o sistema binário seja o “rei da festa” em computação, existe um outro sistema de numeração, designado por sistema hexadecimal, cuja utilidade é igualmente inquestionável.
Este sistema é baseado em 16 símbolos, mais precisamente nos dez algarismos de 0 a 9 e nas seis letras de A a F. Sim, por estranho que possa parecer, são utilizadas letras para representar números! De facto, o “nosso” número 10 é representado pela letra A, o 11 pela letra B, e por aí fora. Quando chegamos ao número 16, esgotamos todos os números hexadecimais com um só dígito e, por isso, representámo-lo através do primeiro número hexadecimal com dois dígitos – o 10. Já o número hexadecimal 7E3 representa o ano em que a ENSICO foi fundada 😉
Embora tenha um aspeto bizarro, este sistema é como o sushi: primeiro estranha-se, depois entranha-se. Ele é utilizado, por exemplo, na identificação de cores em páginas web. Neste formato, cada cor é representada por um código hexadecimal do tipo #RRGGBB, sendo que o valor “RR” é relativo à quantidade de vermelho (Red, em inglês); “GG” reflete a quantidade de verde (Green); e “BB” a quantidade de azul (Blue, em inglês). A título ilustrativo, a cor preta admite o código hexadecimal #000000, pois não possui nenhuma quantidade de vermelho, verde ou azul. Já a cor #0000FF representa um azul “puro”, sem nenhum toque de vermelho ou verde à mistura. Da próxima vez que quiseres elogiar a indumentária da Francisca, sugerimos que digas: “Uau, adoro o tom #FFCE30 da tua saia!”. Pelo menos, é um elogio original 😜

Há, no entanto, um ponto que merece ser esclarecido: quem se lembrou de utilizar um sistema de numeração tão exótico? Porquê 16 símbolos? Há vários motivos que contribuem para esta escolha. Um deles tem a ver com o facto de os computadores manipularem bytes de um lado para o outro, sendo que um byte é simplesmente uma sequência de 8 bits, como 10001111 ou 01010010. Convenientemente, cada dígito hexadecimal representa um número com 4 bits. Logo, cada byte é representado por um número hexadecimal com exatamente 2 dígitos. Por isso, é muito fácil efetuar a conversão entre números binários e números hexadecimais! Por exemplo, ao invés de escrevermos o “comboio” 10001111 em binário, podemos simplesmente escrever o número hexadecimal 8F; já o 01010010 é representado por 52. Trata-se de uma escrita bastante mais económica 😊
É incrível o facto de um mesmo conceito – o conceito de número – admitir tantas materializações diferentes, não é? Algumas delas são mais úteis para os humanos, outras são mais úteis para os computadores, mas todas apresentam as suas vantagens e peculiaridades. Conta-nos lá, se inventasses o teu próprio sistema de numeração, como seria? 😀
Resolução do desafio sobre "Os 3Bs: Bits, Bytes e Basic"
1.a) Qual é o código de 5 bits que representa a letra T?
Resposta: É o código 10011.
1.b) A que letra está associado o código binário 10110?
Resposta: É a letra W.
2. Se o nosso alfabeto tivesse 126 letras ao invés de 26, quantos bits seriam necessários para representar cada letra, recorrendo a uma árvore binária?
Resposta: Seriam necessários 7 bits, uma vez que 26 < 126 = 27.
Colaboração de Mano a Mano Graphic Design Club
[Às quintas-feiras, o PÚBLICO na Escola dá espaço às ciências da computação, numa parceria com a ENSICO - Associação para o Ensino da Computação.]
No vídeo de hoje, a Embaixadora da ENSICO e Master Teacher, Inês Guimarães (a conhecida Youtuber MathGurl), explica o modo como funcionam vários sistemas de numeração, incluindo o sistema binário.
Assiste ao vídeo para compreenderes melhor o modo como os computadores representam os números com que lidamos no dia-a-dia. E, se fores um fã incondicional do Baby Yoda, não podes mesmo perder esta explicação! 😜
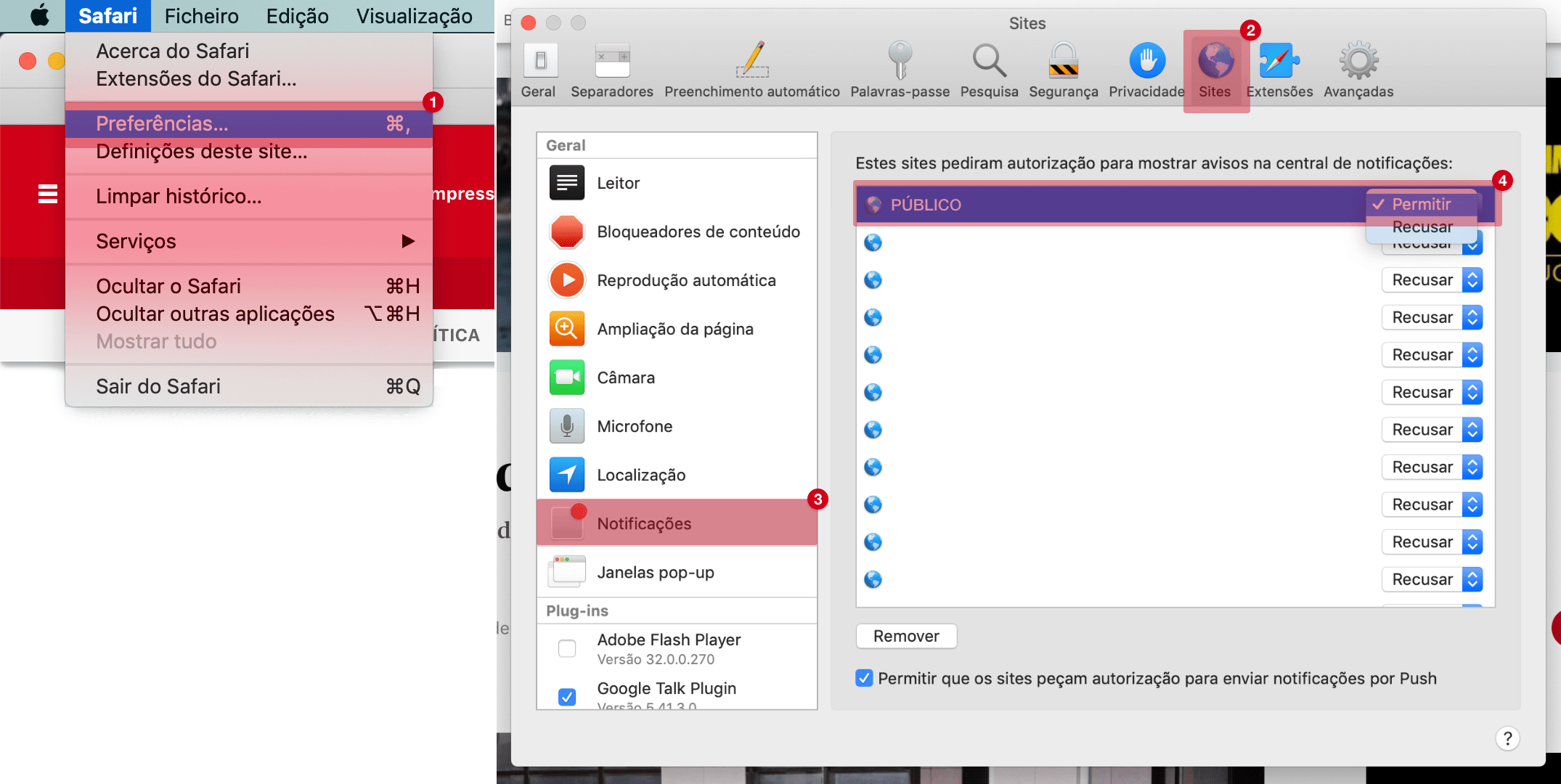
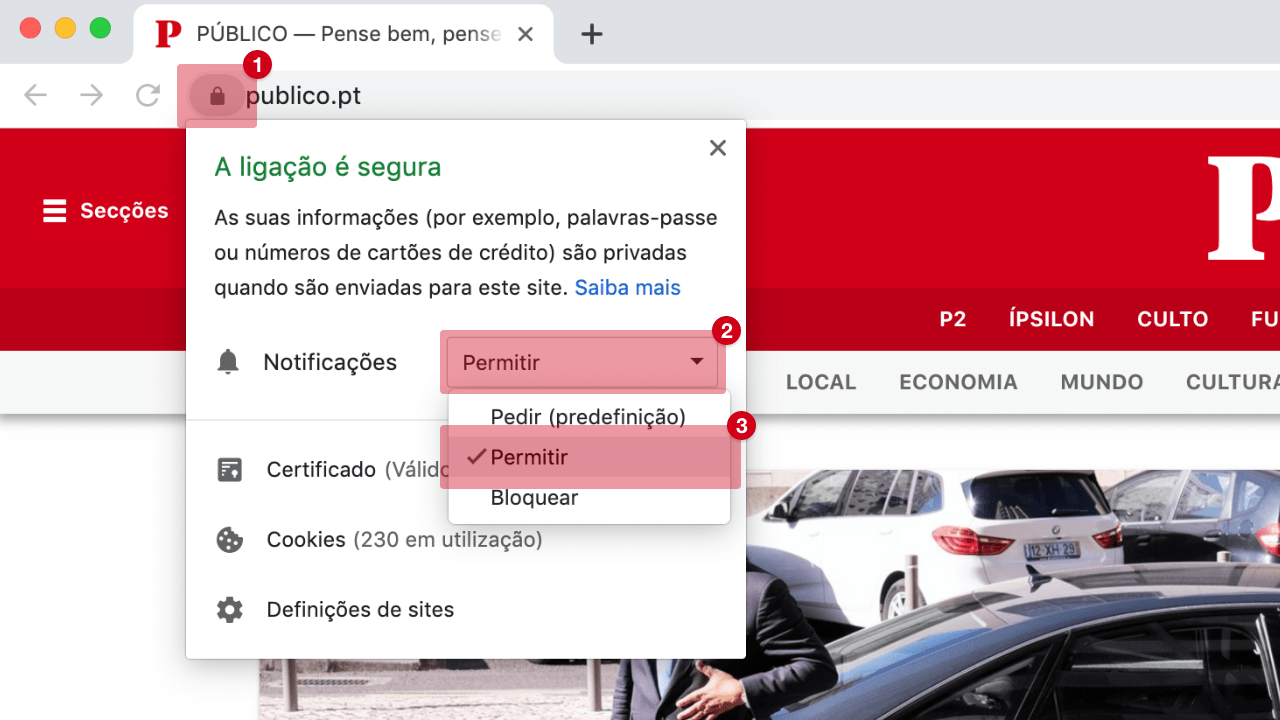
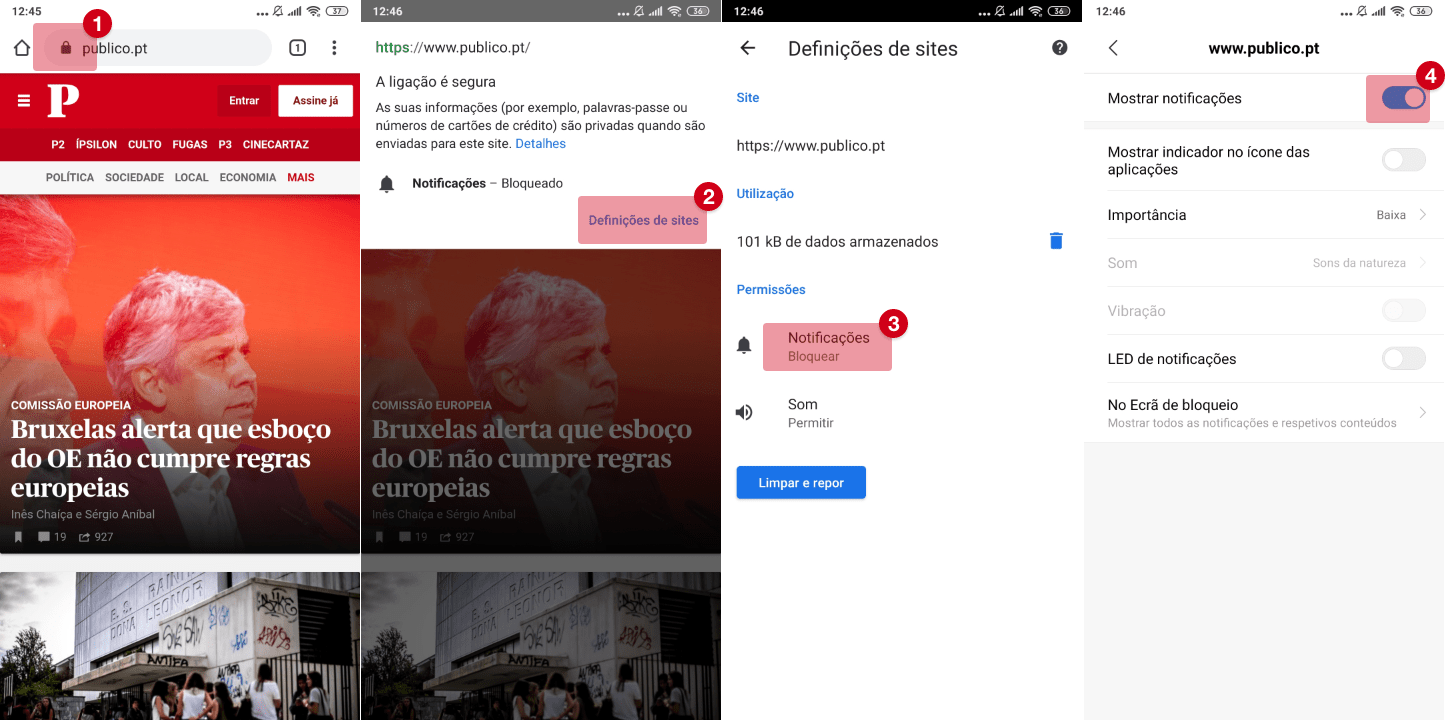
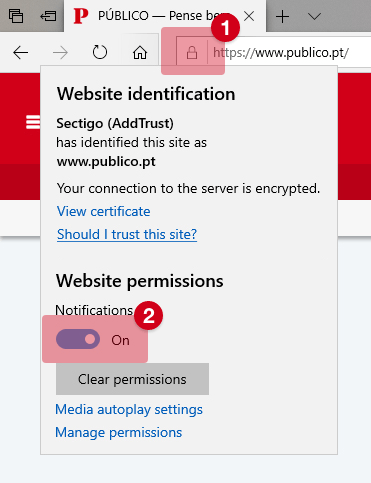
Gerir notificações
Estes são os autores e tópicos que escolheu seguir. Pode activar ou desactivar as notificações.
Gerir notificações
Receba notificações quando publicamos um texto deste autor ou sobre os temas deste artigo.
Estes são os autores e tópicos que escolheu seguir. Pode activar ou desactivar as notificações.
Notificações bloqueadas
Para permitir notificações, siga as instruções: