COMPUTAÇÃO NA ESCOLA
Os 3Bs: Bits, Bytes e Basic
Se nasceste nos anos 2000, provavelmente não imaginas como era o mundo antes da invenção dos telemóveis, dos computadores e da internet... mas acredita que já existia vida na Terra!
ENSICO(Texto)
Hoje vamos fazer uma viagem ao passado e “aterrar” nos loucos anos 80. Por isso, recomendamos que leias o resto do artigo ao som de Madonna ou Michael Jackson 😉

Os anos 80 foram um marco na popularização da informática. Altair 8800 (1975), BBC Micro (1981), IBM PC (1981) e ZX Spectrum (1982) são alguns exemplos dos “aparelhos” que alimentaram a imaginação de toda uma geração de jovens ávidos por jogos cada vez mais sofisticados e, acima de tudo, por poder criar os seus próprios jogos e os seus próprios programas de computador! Do lado do software, mais concretamente dos Sistemas Operativos, o Xenix (1981), o MS-DOS (1981) e o “Classic” Mac OS (1984) vinham tornar a utilização destes aparelhos acessível a todos aqueles que quisessem ter acesso a essa “oitava maravilha” do mundo chamada “computador”.
Essa onda de entusiamo trouxe consigo palavras inglesas que se tornaram tão correntes que foram rapidamente adotadas por todas as línguas. Falamos dos 3Bs: Bits, Bytes e Basic. Bits e Bytes identificam unidades de informação binária; Basic (1964) identifica a linguagem de programação, básica e acessível, “incorporada” nos computadores que já se compravam facilmente em lojas de eletrónica ou até mesmo em lojas de eletrodomésticos. As suas versões Sinclair BASIC (1979, desenvolvida para o ZX80), BBC BASIC (1981, desenvolvida para o BBC Micro) e BASIC-80 (1981, desenvolvida para o Altair 8800) deram início aos “anos loucos” da programação e alavancaram a explosão da Era Digital em que vivemos 😏

Comecemos por explorar o nosso primeiro “B”. Como sabes, o bit é a unidade mínima de informação que pode ser transmitida ou armazenada, podendo tomar apenas dois valores: 0 ou 1. De facto, qualquer informação (como este texto que estás a ler) é representada num computador através de bits. Mas, por exemplo, como serão representadas as várias letras do alfabeto através de 0s e 1s? 🤔
Se o alfabeto consistisse apenas nas letras A e B, seria muito simples: bastaria associar ao A um 0 e ao B um 1, como se mostra nesta imagem.
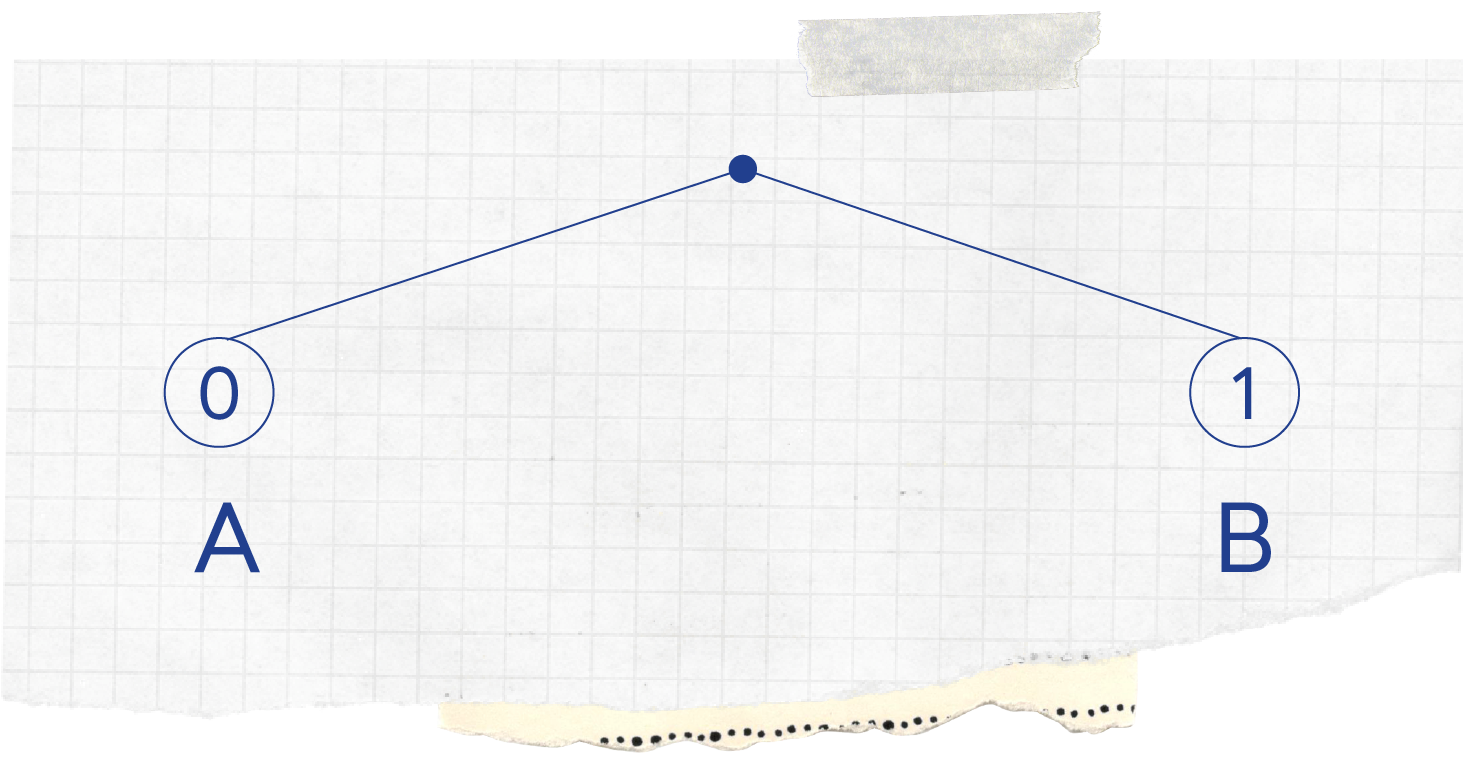
Repara que partimos de um ponto no espaço e desenhamos dois "ramos", um com um 0 para a esquerda e outro com um 1 para a direita. Mas o que nós verdadeiramente queremos é poder representar palavras, como por exemplo “ABACATE”. Para isso acontecer, o que vamos fazer a seguir é repetir esse processo para o 0 e para o 1, como podemos ver nesta próxima figura.
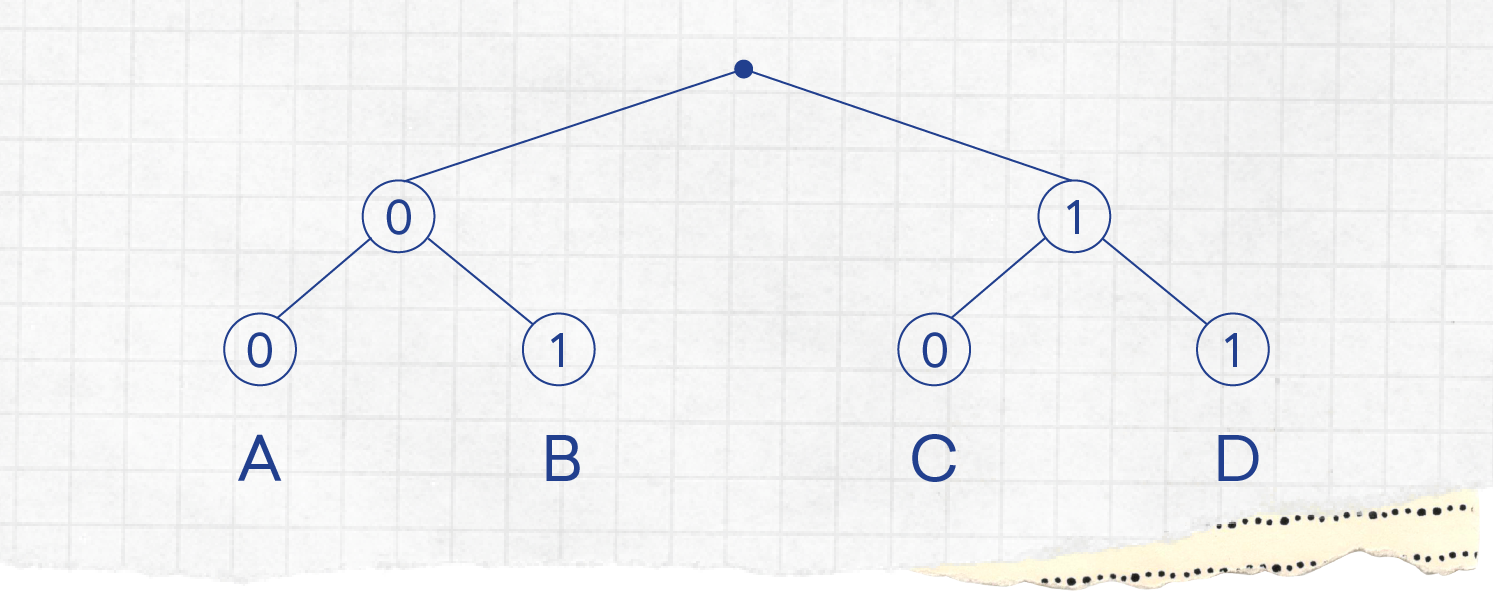
Agora já temos uma figura com 4 "folhas", o que nos permite chegar ao D. A estes diagramas constituídos por vários "ramos" damos o nome de árvores. E, neste caso particular, o que temos são árvores binárias, pois cada ramo divide-se em dois.
Vamos então pensar: se 4 “folhas” nos permitiram chegar ao D, será que mais “folhas” nos permitirão alcançar ainda mais letras? A resposta é simples e é SIM! 😁 E o processo continua também a ser simples: basta repetir o que fizemos para cada 0 e 1 que ainda não tem "filhos", conforme podemos ver na imagem que se segue. Assim já conseguimos chegar do A ao H! As letras são 8, uma por cada "neto".
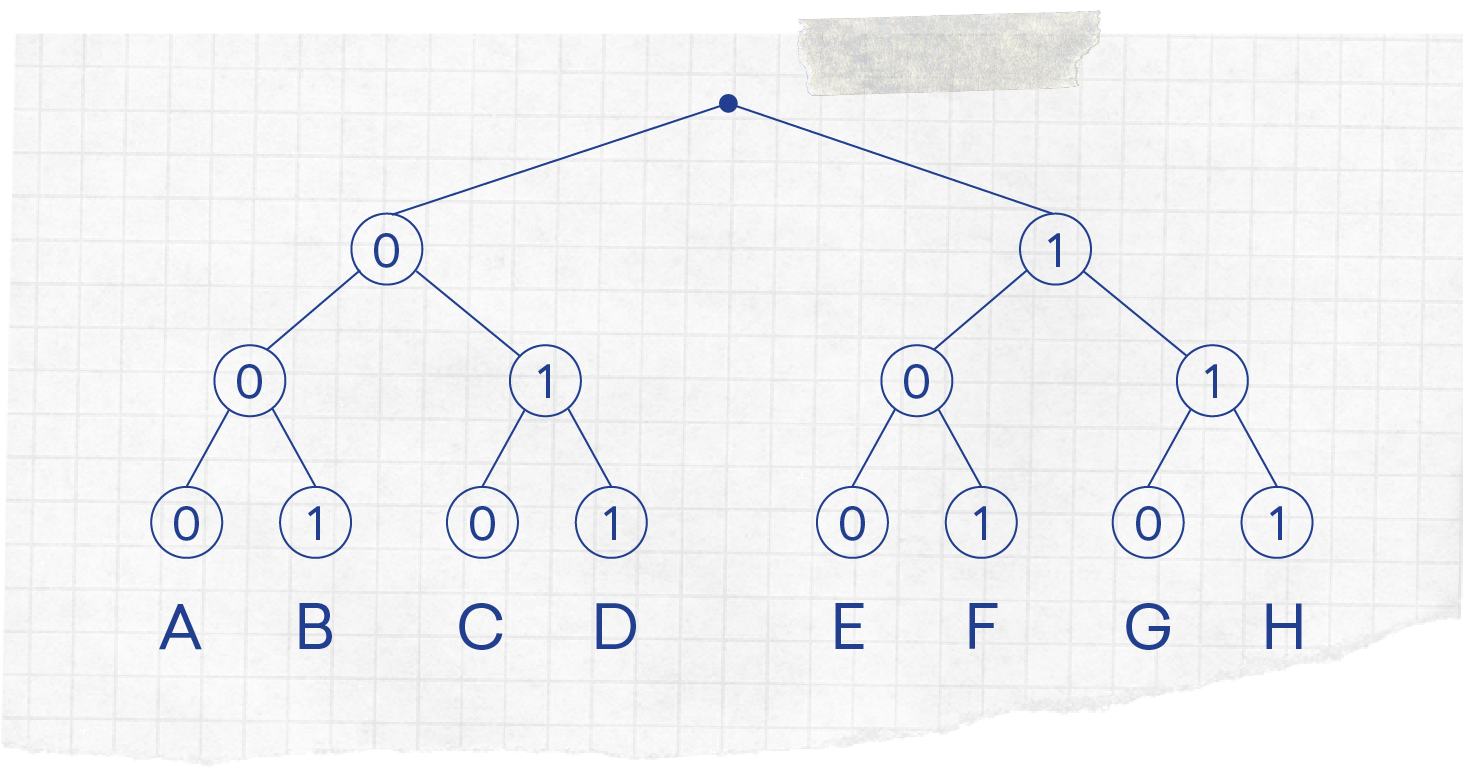
Agora que temos mais letras, e que sabemos o que fazer para termos ainda mais, surge a pergunta: que 0s e 1s estão associados a cada letra? O que temos é apenas um desenho, mas é costume dizer-se que desenhos valem mais que mil palavras... 😋

Em homenagem a alguns dos nossos antepassados navegadores, vamos então levantar âncora, navegar ao vento e, quem sabe, percorrer assim os caminhos que nos permitirão encontrar as letras que conhecemos bem e que nos foram deixadas por antepassados ainda mais longínquos...
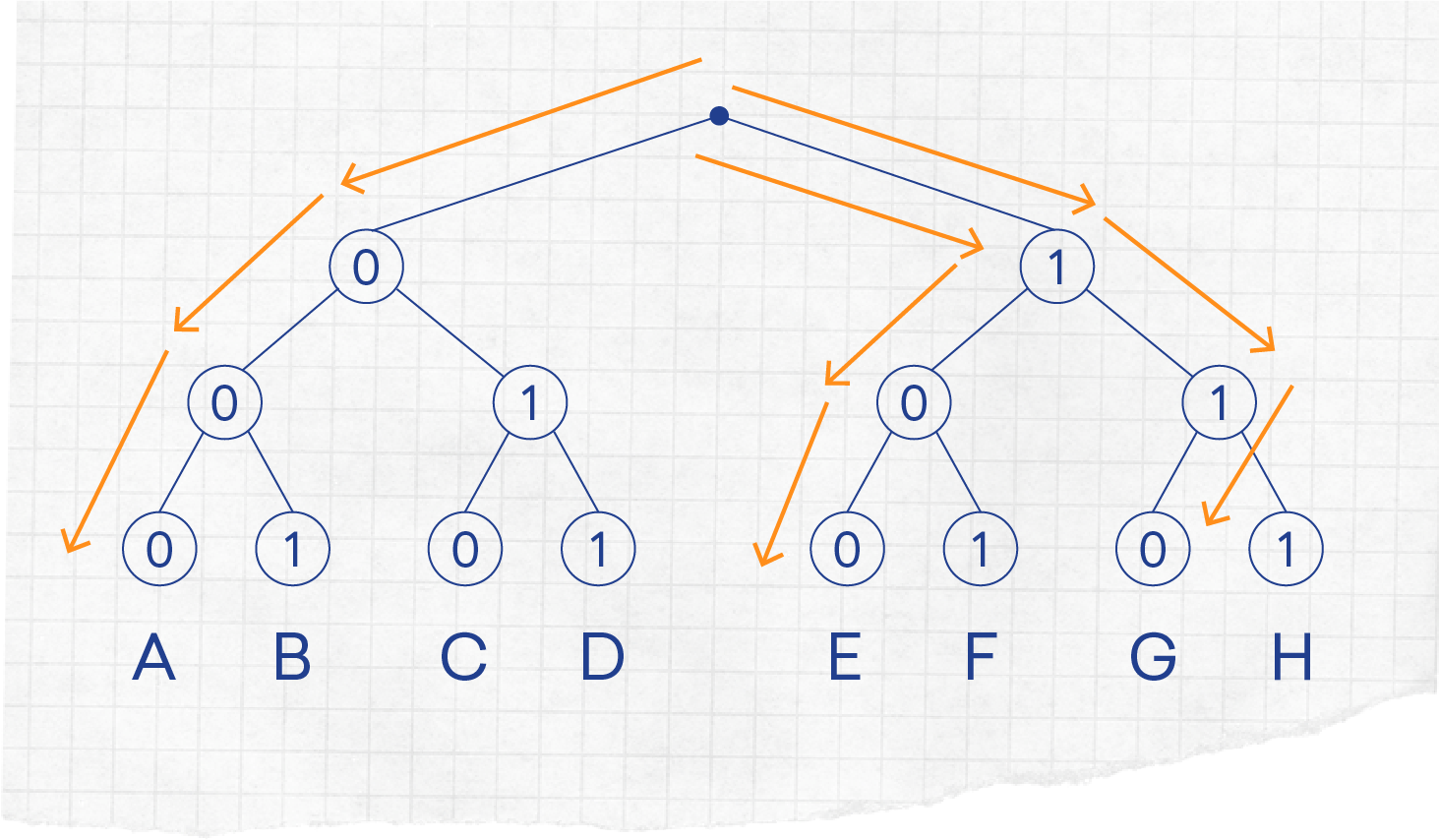
Comecemos pela letra A: qual é o caminho que se tem de seguir para ir do ponto de partida (o topo da árvore) até essa letra? É só seguir o caminho “pintado a laranja”: primeiro passamos por um 0, depois por outro 0 e finalmente... outro 0! Em suma, à letra A está associado o caminho 000. Vamos agora repetir o que fizemos para a letra E, por exemplo. Começando em cima, como atrás, visitamos primeiro um 1, depois um 0 e finalmente outro 0, o que dá o caminho 100. Logo, a letra E corresponde ao caminho 100. E para a letra G temos o caminho 110, etc.
Qual foi a principal limitação? Não conseguimos representar as letras todas! Mas isso não é problema, basta continuar e acrescentar mais níveis: bisnetos, trinetos... E para conseguirmos chegar até ao Z, precisamos de uma árvore com 5 níveis. Got it? 😄
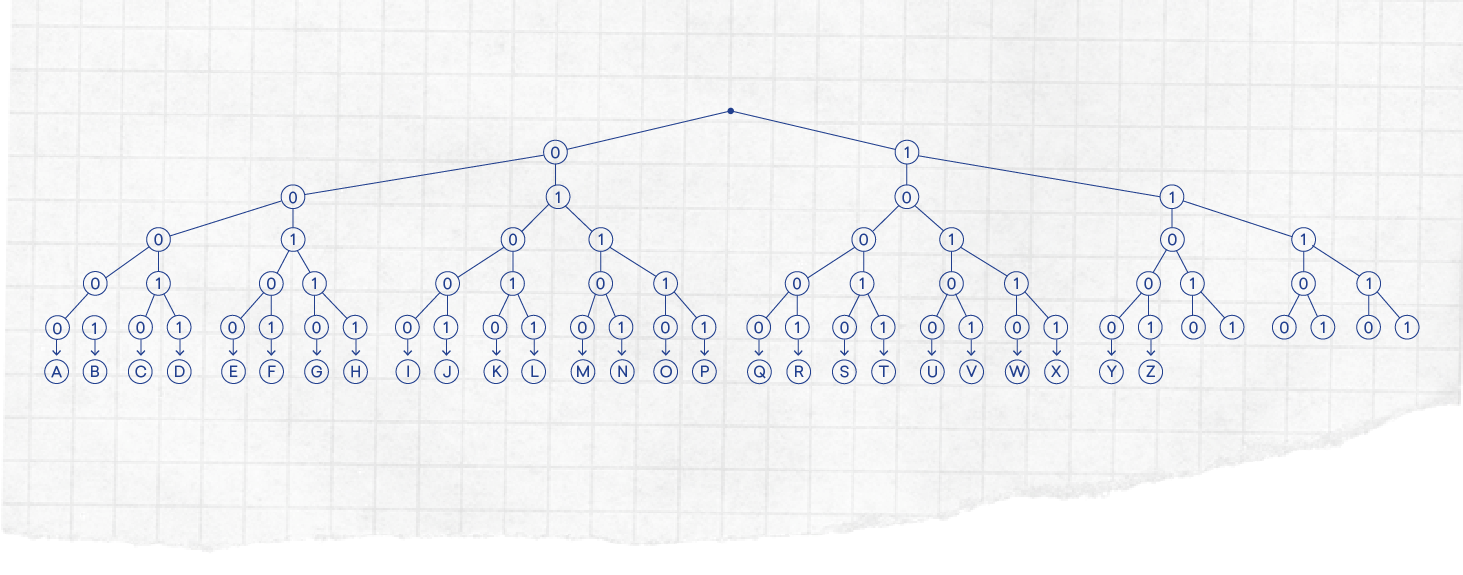
1. Recorre a esta última árvore binária para responderes às seguintes questões.
a) Qual é o código de 5 bits que representa a letra T?
b) A que letra está associado o código binário 10110?
2. Se o nosso alfabeto tivesse 126 letras ao invés de 26, quantos bits seriam necessários para representar cada letra, recorrendo a uma árvore binária?
Mas será que, nos computadores, as letras são representadas por 5 bits, como vimos naquela última árvore? Não! 😝 Os códigos binários padrão utilizados na representação de letras e outros caracteres têm variado ao longo dos anos. Mas um que é bastante consensual é o chamado código ASCII.
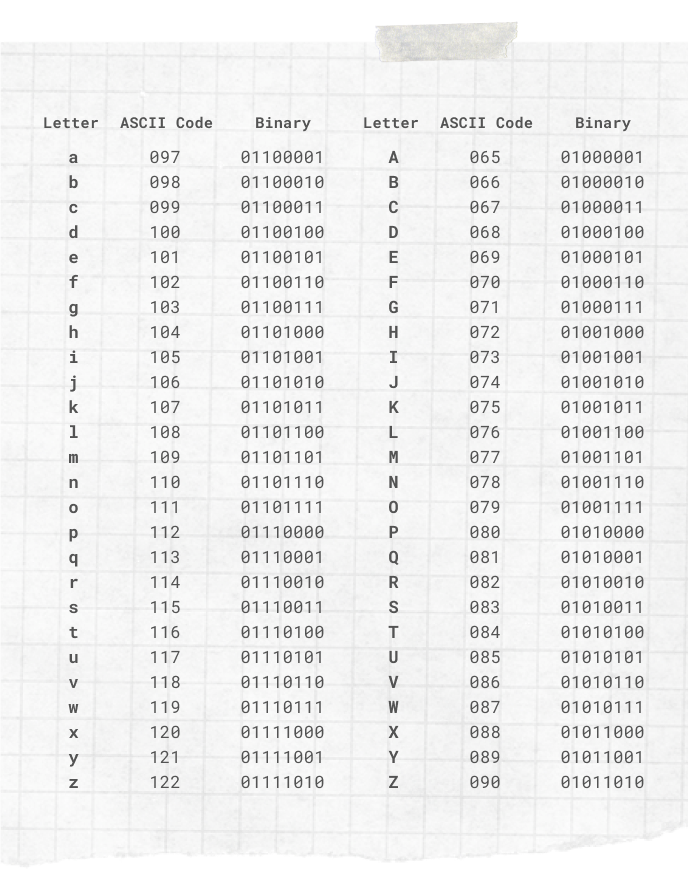
No código ASCII, cada letra é representada por 8 bits. Por exemplo, o código ASCII da letra D é 01000100. Os outros caracteres (números, sinais de pontuação, etc.) são também representados de forma análoga. E assim chegamos ao segundo “B” dos 3Bs: a uma sequência de 8 bits dá-se o nome de byte. Assim, no código ASCII, a cada letra ou qualquer outro caracter corresponde um byte 😀
E repara como, ainda hoje, os bits e os bytes continuam a ser as unidades utilizadas para identificar a capacidade de processamento e armazenamento dos computadores. O teu telemóvel, por exemplo, tem uma capacidade de armazenamento de dezenas de gigabytes (GB), ou seja, dezenas de milhares de milhões de bytes! 🤯 E o teu computador trabalha, seguramente, com um sistema operativo de 32 ou 64 bits.
Mas nem sempre foi assim...
Se fizeste o que sugerimos no início deste artigo, se estás já com o som de Madonna ou Michael Jackson entranhado na tua cabeça e se estás com vontade de programar um jogo de naves espaciais como o do Space Invaders, prepara-te então para isto! Vamos finalmente falar-te do terceiro “B” dos 3Bs 😀
Altair 8800, BBC Micro, IBM PC, ZX Spectrum, recordas-te? Falamos deles no início deste artigo e eram todos computadores munidos de microprocessadores de 8 bits. A linguagem de programação BASIC, que se tornou tão popular nessa altura, era incorporada “de raiz” em muitos desses computadores que passaram a ser cada vez mais “pessoais”. Sim, sim, é por isso que ainda hoje falas do “teu” PC, “Personal Computer”, ou seja, um “Computador Pessoal” acessível ao comum dos mortais. E para tornar a linguagem BASIC tão, mas tão acessível, chegou a ser incorporada nos teclados. E agora, adivinha lá, como terá sido isso possível? Se pensaste novamente na tabela ASCII, pensaste muito bem e acabaste de realizar a tua viagem ao passado. Só te falta o skate, a revista BYTE debaixo do braço e um ZX Spectrum para te poderes considerar um jovem dos anos 80 😎

Pensa no seguinte: sendo a tabela ASCII composta por códigos de 8 bits, quantas “coisas” conseguimos então representar? Por outras palavras, se o número de níveis das “árvores binárias” que vimos atrás indica o número de bits utilizados na codificação binária, uma árvore com 8 níveis quantas “folhas” tem no total? É isso mesmo, 256 ou 28, podendo por isso representar 256 “coisas” diferentes. Se agora somares o número de letras (maiúsculas e minúsculas), números e restantes símbolos que normalmente vês nos teclados de qualquer computador, rapidamente te aperceberás que ficas sensivelmente com metade da tabela por preencher. É precisamente essa metade que permite estender a tabela ASCII original (de 7 bits apenas) com outras “coisas” e é, por isso, designada, em rigor, por “Extended ASCII Table”. Em resumo, a tabela ASCII conforme a conhecemos hoje inclui: uma primeira parte, designada por “ASCII control characters”, cujos códigos (em decimal) vão do 0 ao 31; uma segunda parte, designada por “ASCII printable characters”, cujos códigos (em decimal) vão do 32 ao 127; e uma terceira parte, designada por “The Extended ASCII codes”, cujos códigos (em decimal) vão do 128 ao 255. Observa que para representar a primeira e a segunda parte são necessários apenas códigos de 7 bits; já para as 3 partes são necessários códigos de 8 bits. Entendido? 😉
Repara agora na impressão do que está associado à Tabela ASCII definida no célebre computador ZX Spectrum. Para além das letras, números e símbolos que conheces bem, a partir de determinada altura vês também “palavras” que fazem parte da linguagem BASIC: RND, INKEY$, PI, FN, POINT, SCREEN$, ATTR, etc. Podes aliás encontrar a lista completa de “palavras” – comandos, funções, operadores lógicos, etc. – da linguagem aqui.
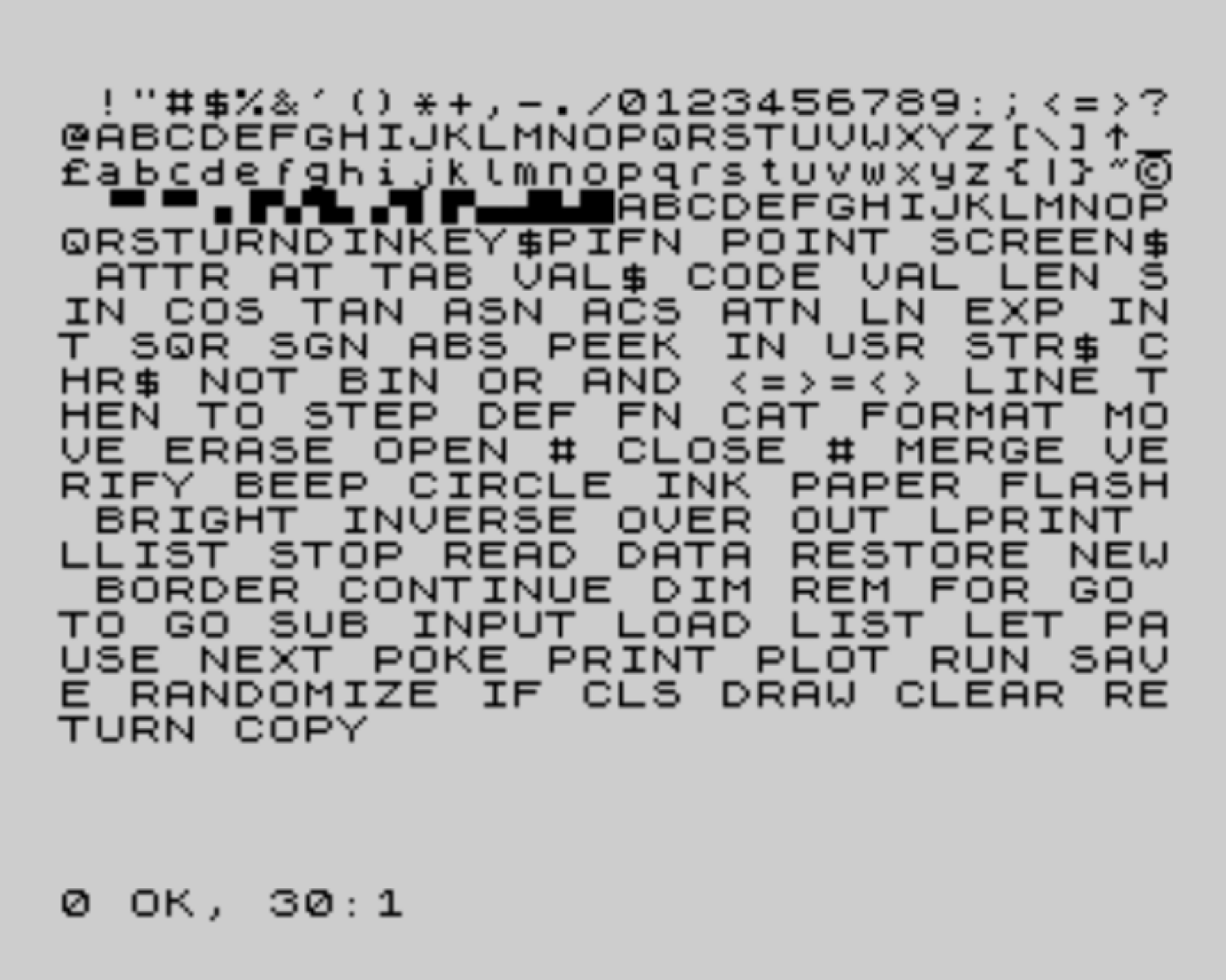
Observa com atenção estas duas últimas imagens. Vês como a linguagem BASIC está “impressa” no teclado do ZX Spectrum? Não foi por acaso que esta máquina, com cerca de 5 milhões de unidades vendidas em todo o mundo, se tornou um verdeiro ícone dos anos 80. Como nenhuma outra, combinou e tornou acessível a toda uma geração o poder dos 3Bs. E é por isso, e ainda hoje, um símbolo da criatividade que abriu as portas de um novo mundo a toda uma geração. Agora é a tua vez! Continua connosco e conhecerás cada vez melhor esse novo mundo que se abriu e que é o teu: o mundo da computação 😀 Até à próxima semana!
Colaboração de Mano a Mano Graphic Design Club
[Às quintas-feiras, o PÚBLICO na Escola dá espaço às ciências da computação, numa parceria com a ENSICO - Associação para o Ensino da Computação.]
O João Diogo Ramos é um colecionador apaixonado por todo o fenómeno ZX Spectrum. Fundou o museu LOAD, dedicado ao ZX Spectrum, aquele que foi o “primeiro computador” para muitos portugueses e estrangeiros.
O museu, localizado em Cantanhede, ajuda todos os que o visitam a compreender o decisivo papel do ZX Spectrum na revolução tecnológica que se seguiu e que permitiu, por exemplo, colocar um telemóvel no nosso bolso. Permite também descobrir o importante papel desempenhado pela equipa portuguesa da TIMEX neste fenómeno iniciado nos anos 80.
Convidamos o João Diogo para nos falar deste período tão fascinante da história da computação e do contributo decisivo de Sir Clive Sinclair (1940 – 2021) para que os computadores se tornassem aparelhos de consumo doméstico.
Ao estado S1 chegam todas as palavras bcesas terminadas em A.
Ao estado S2 chegam todas as palavras bcesas terminadas em C.
Ao estado S3 chegam todas as palavras bcesas terminadas em B.
Ao estado N chegam todas as palavras contendo pelo menos um C que não é precedido por nenhum B.
Gerir notificações
Estes são os autores e tópicos que escolheu seguir. Pode activar ou desactivar as notificações.
Gerir notificações
Receba notificações quando publicamos um texto deste autor ou sobre os temas deste artigo.
Estes são os autores e tópicos que escolheu seguir. Pode activar ou desactivar as notificações.
Notificações bloqueadas
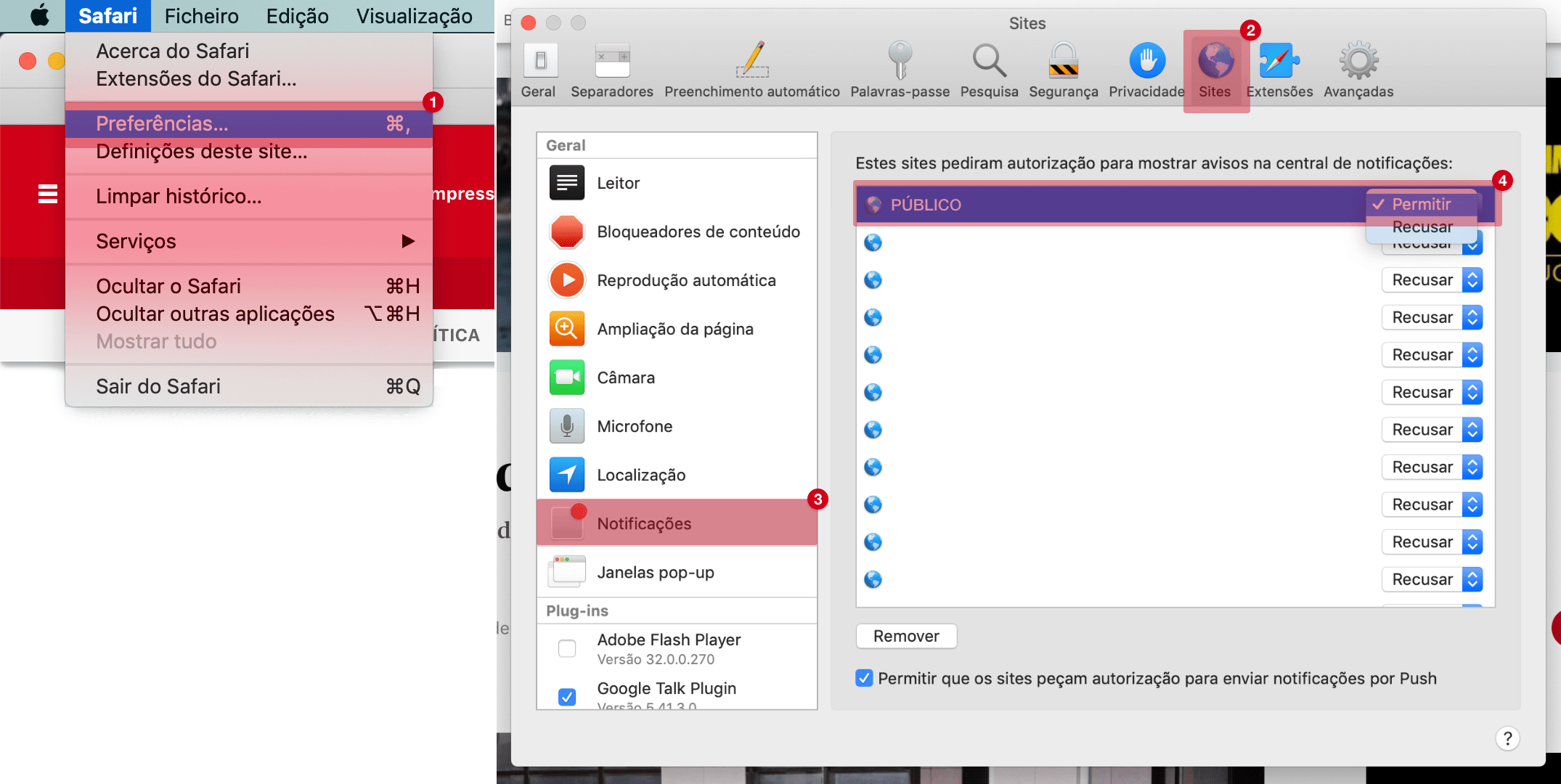
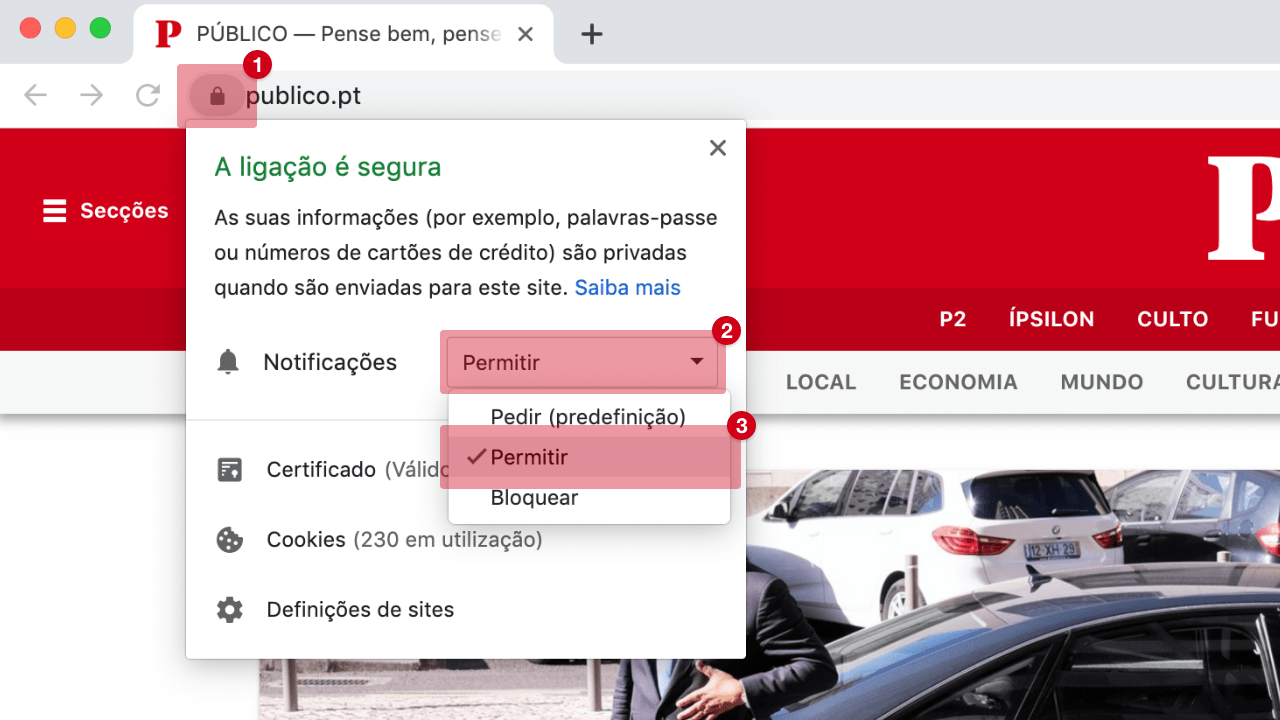
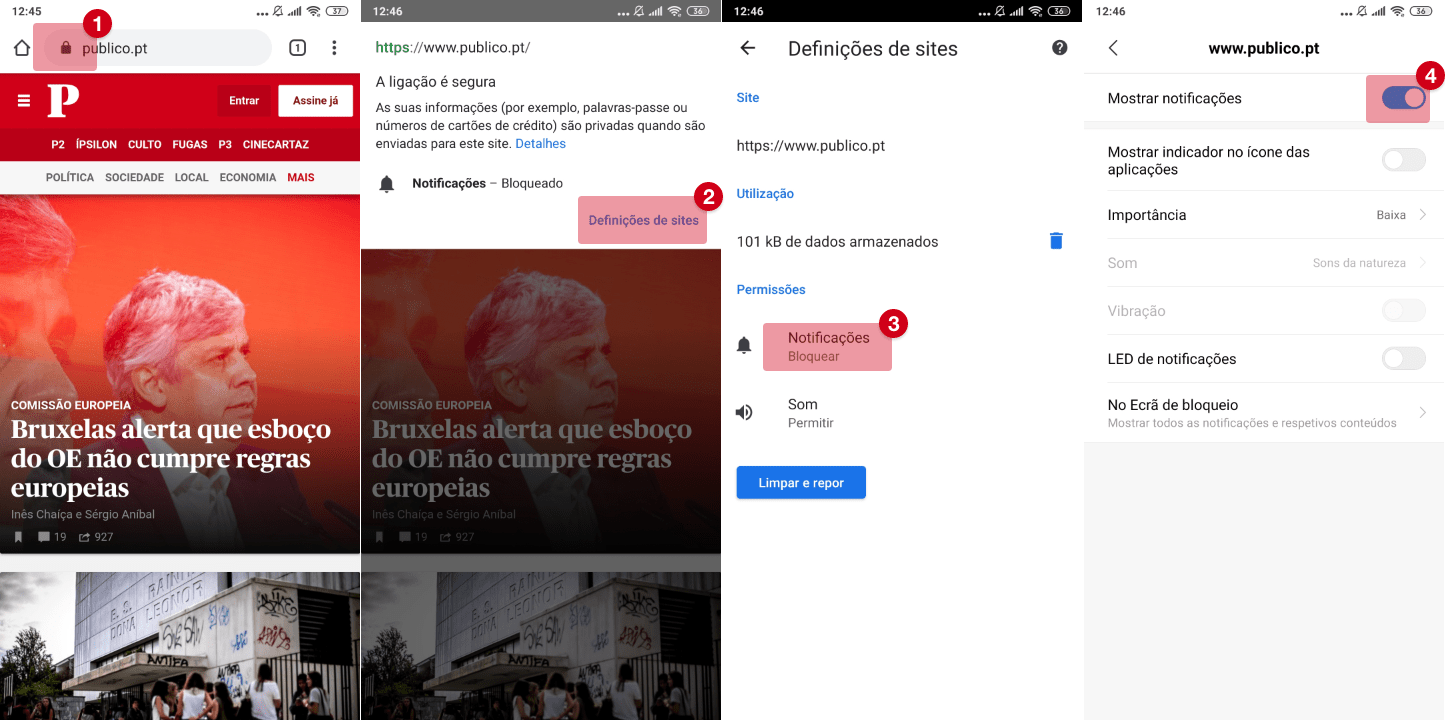
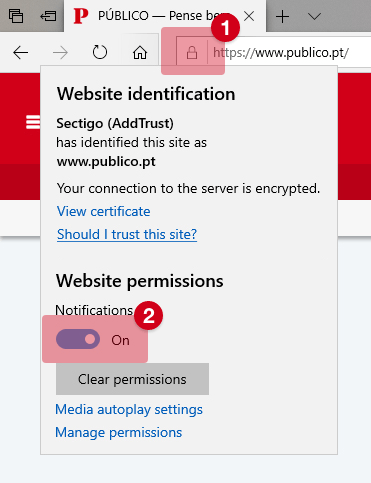
Para permitir notificações, siga as instruções: