COMPUTAÇÃO NA ESCOLA
Compressão de Dados
No filme "Querida, Eu Encolhi os Miúdos”, o cientista Wayne encolhe acidentalmente os seus dois filhos, e o processo para os trazer de volta ao tamanho original é tudo menos simples. Neste artigo, vamos ver como podemos “encolher” ficheiros, algo semelhante ao que Wayne faz no filme… mas que não tem nada a ver 🤪
ENSICO(Texto)
Certamente já te cruzaste com ficheiros .zip ou .rar ao fazer transferências da internet, e até já ouviste dizer que estes formatos de ficheiros são top porque ocupam menos espaço no computador. Mas o que está por detrás de tudo isto, mesmo? 🤔

Com o passar dos anos, os dispositivos eletrónicos que utilizamos têm vindo a apresentar uma capacidade de armazenamento cada vez maior. Por incrível que pareça, o IBM Simon (1995), considerado o primeiro smartphone da História, tinha uma capacidade de armazenamento de apenas 1 MB. No entanto, atualmente, ninguém fica satisfeito com um telemóvel que tenha menos de 64 GB de memória, um valor 64 000 vezes superior ao que mencionamos anteriormente.
Ainda assim, volta e meia lá vêm os nossos dispositivos queixarem-se que têm pouco espaço de armazenamento, que estão já a ficar cheios de entulho... e lá temos nós de apagar aquele vídeo da nossa prima a dançar no Natal de 2017, que sinceramente nem sabemos bem o que ainda lá está a fazer. Desta forma, continua a ser muito importante o desenvolvimento de métodos que permitam reduzir o tamanho de um ficheiro sem alterar (ou alterando muito pouco) a informação nele contida.
O objetivo da compressão de dados é precisamente modificar a forma como a informação é armazenada num dispositivo de modo a ocupar menos espaço. Existem essencialmente dois tipos de compressão – a compressão com perdas (lossy) e a compressão sem perdas (lossless). Mas antes de explicarmos o significado destes termos, ainda temos tempo para fazer uma piada seca:

Agora, sem mais demoras, vamos mergulhar então no lago da compressão 😉
Compressão lossy
A compressão lossy, i.e. com perda de informação, é frequentemente utilizada em ficheiros de imagem, vídeo e áudio. De grosso modo, significa que “aldrabamos” um bocadinho a informação original do ficheiro de forma a diminuir o seu tamanho. É um processo que envolve alguma perda de informação, mas que é praticamente impercetível para os sentidos humanos.
Por exemplo, nas imagens abaixo, a da direita ocupa praticamente metade do espaço no computador comparativamente com a da esquerda e, no entanto, os “estragos” causados pela perda de informação quase não são percetíveis a olho nu no ecrã.

No artigo sobre representação de imagens a cor, dissemos que cada píxel colorido de uma imagem ocupa 3 bytes no computador, pois cada uma das quantidades de vermelho, verde e azul da respetiva cor é representada por 1 byte. Ora, a imagem da esquerda possui 640 × 400 = 256 000 píxeis, logo, pelo que dissemos, deveria ocupar 256 000 × 3 = 768 000 bytes em memória, ou seja, 750 KB. No entanto, se formos consultar a informação do ficheiro, vemos que o seu tamanho é de apenas 98 KB, uma vez que a imagem já passou por um processo de compressão, recorrendo ao famoso método JPEG.
De facto, o JPEG é um algoritmo de compressão de imagens digitais que, ao ser aplicado, produz ficheiros com as extensões .jpeg ou .jpg, tipicamente. É a técnica mais utilizada no mundo no que diz respeito à compressão lossy de imagens, tendo contribuído para a disseminação maciça de fotografias (de gatinhos e não só...) na internet e, em particular, nas redes sociais 😊

Compressão lossless
Embora nos possamos dar ao luxo de perder alguma informação quando comprimimos imagens ou vídeos, o mesmo não acontece quando estamos a lidar com textos ou programas de computador, por exemplo. Se o código de um dos programas do computador da Apollo 11 tivesse sido comprimido e acidentalmente se tivesse perdido um único bit no meio de milhões, se calhar o dia 20 de julho de 1969 teria acabado de forma diferente... Além disso, seria muito desagradável enviares uma mensagem a alguém e, após passar por um processo de compressão, ocorrer o desaparecimento de uma palavra – a informação que querias passar poderia chegar completamente distorcida! 😱
Assim, nestes casos, os métodos de compressão lossy não são adequados. A informação original do ficheiro a comprimir tem de ficar intacta e, por isso, é necessário proceder a uma compressão lossless, i.e. sem perda de informação. Mas como será possível mantermos exatamente a mesma quantidade de informação a transmitir e, ao mesmo tempo, reduzirmos a quantidade de informação armazenada?! 🤯 Isto faz lembrar o truque do quadradinho de chocolate que desaparece mantendo a tablete com o seu tamanho original...
Vamos agora explicar uma “magia” de compressão lossless conhecida por codificação de Huffman. Como irás ver, o segredo está na forma como escolhemos representar uma determinada informação utilizando 0s e 1s, os bits de um computador. Diferentes representações conduzem a ficheiros com diferentes tamanhos!
A forma mais fácil de compreenderes este método é através de um exemplo. Imagina que queres enviar a um amigo a mensagem

É uma mensagem um pouco bizarra, mas não te julgamos... Além disso, a mensagem tem de ser transmitida através de 0s e 1s, e cada um destes bits custa 1€ a ser enviado (andam caros os bits!).
Para pagares o mínimo possível, o melhor é ignorares os espaços e sinais de pontuação, enviando a mensagem mais curta

A questão é: como devemos codificar as letras desta mensagem, através de 0s e 1s, de forma a pagar o mínimo possível? Repara que este é um problema de compressão de texto, pois queremos utilizar o menor número de bits para codificar uma mensagem (e, assim, ocupar menos espaço no computador).
Por exemplo, se utilizássemos a codificação ASCII (estendida), iríamos representar cada letra através de uma sequência de 8 bits. Logo, como a mensagem tem 22 letras no total, iríamos gastar 22 × 8 = 176€. Credo! Temos mesmo de procurar uma alternativa mais económica... 😰
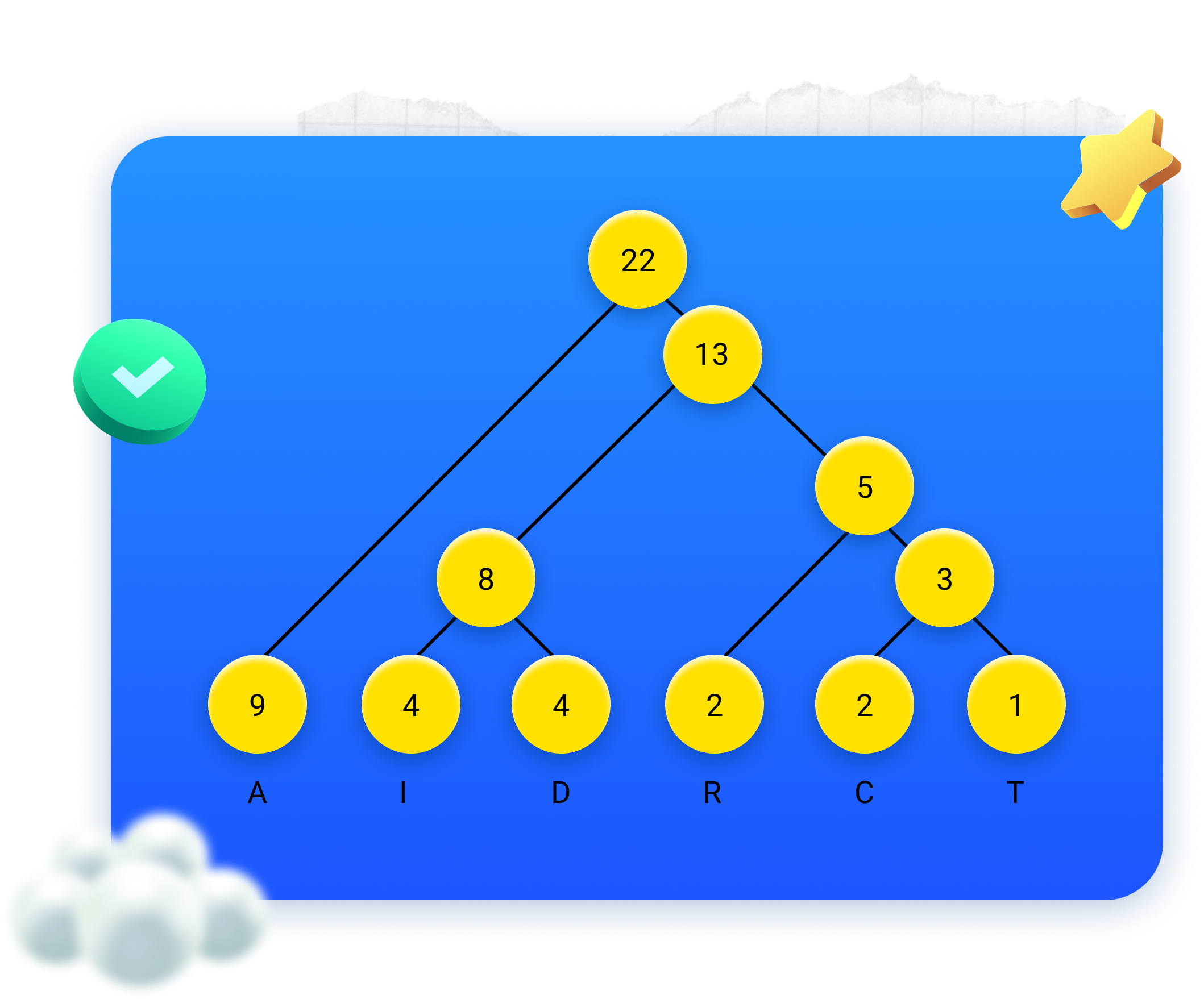
Vamos então aplicar a codificação de Huffman para atribuir um código de 0s e 1s a cada uma das letras A, C, D, I, R, T que constam na mensagem – afinal, são só essas letras que nos interessam. O primeiro passo é contar quantas vezes cada letra surge em "ACADADIAATIADACRIADARI". Obtemos as seguintes frequências:
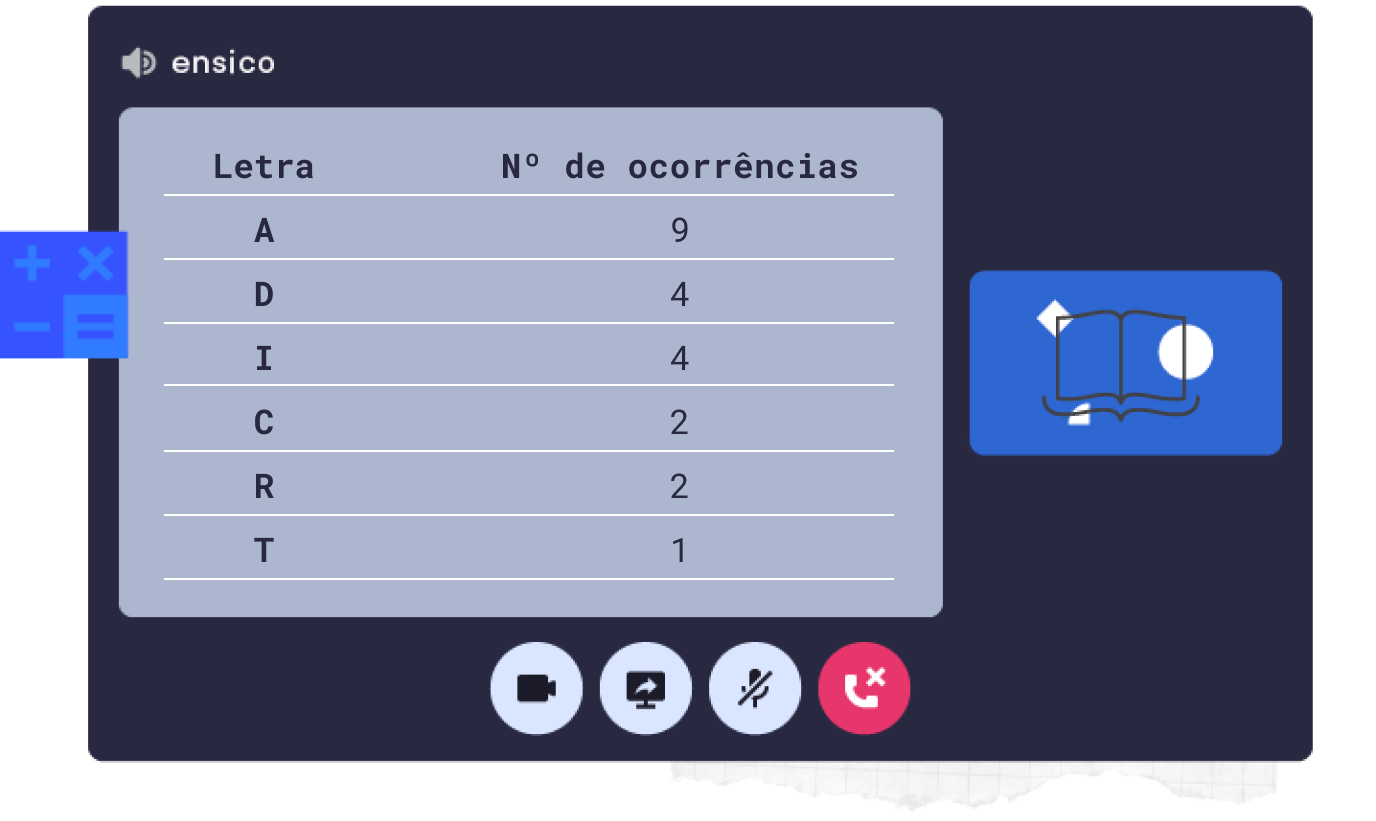
De seguida, escrevemos as letras da mais frequente para a menos frequente, registando a frequência de cada uma num círculo azul.
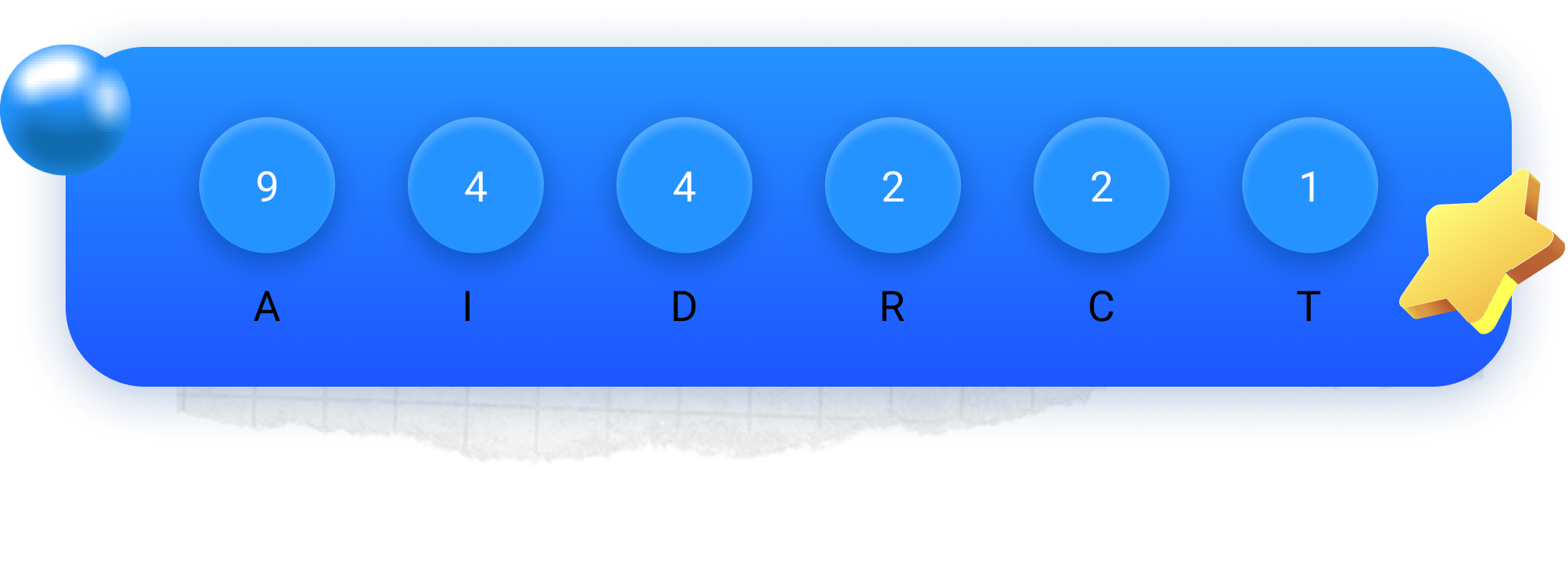
Após escrever as letras e respetivas frequências, procedemos do seguinte modo:
Passo 1: unir os dois menores valores a azul.
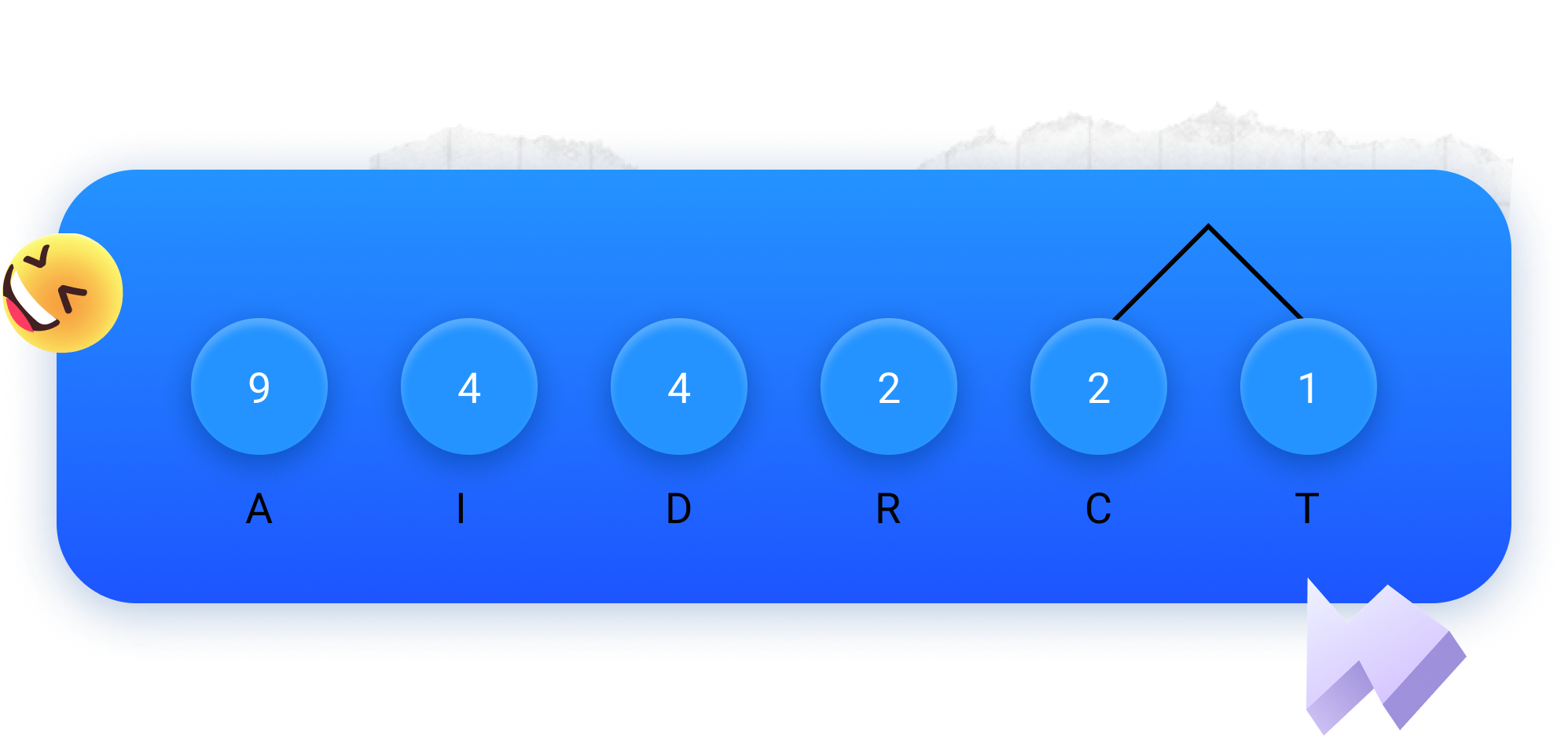
Passo 2: pintar os valores unidos com amarelo.
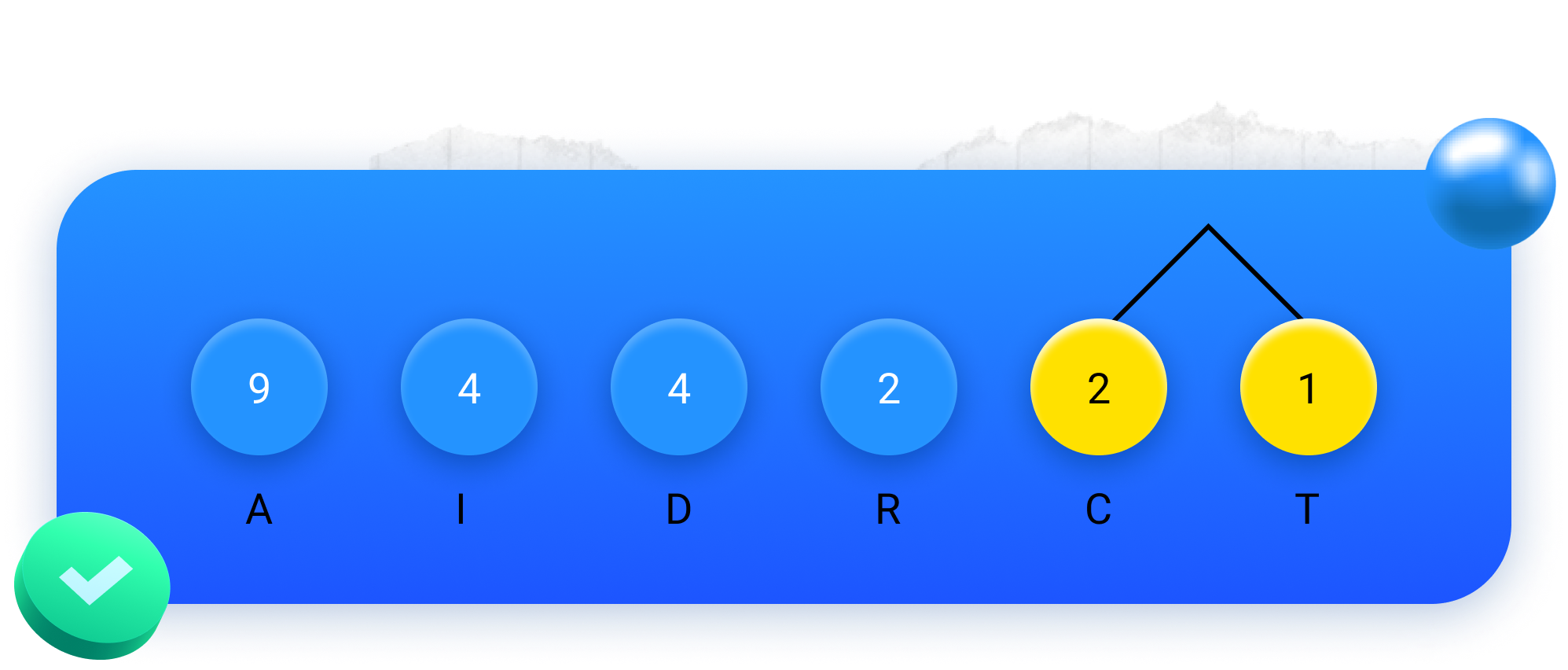
Passo 3: desenhar um círculo azul com a sua soma.
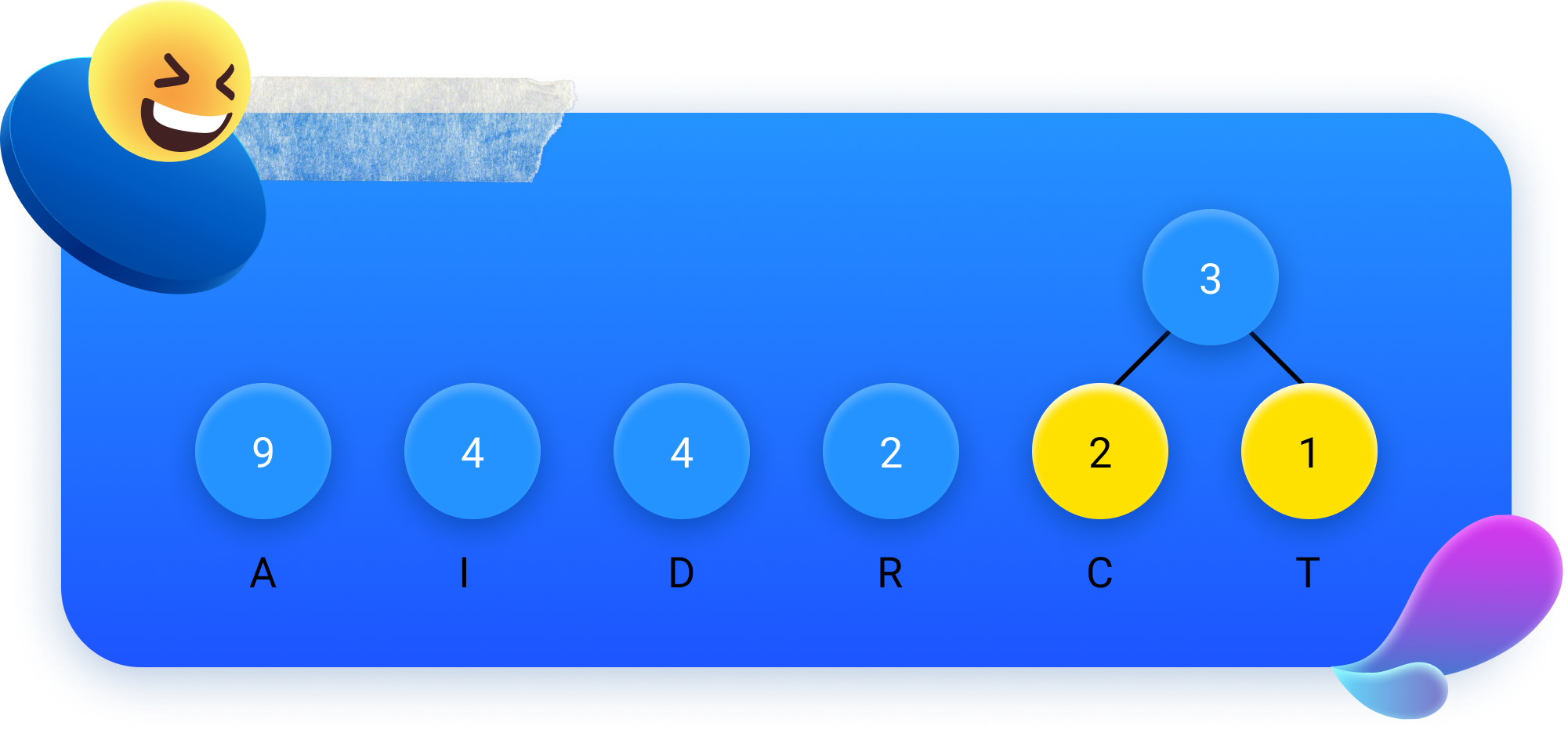
Depois, é só repetir! Voltamos a unir os dois menores valores a azul...
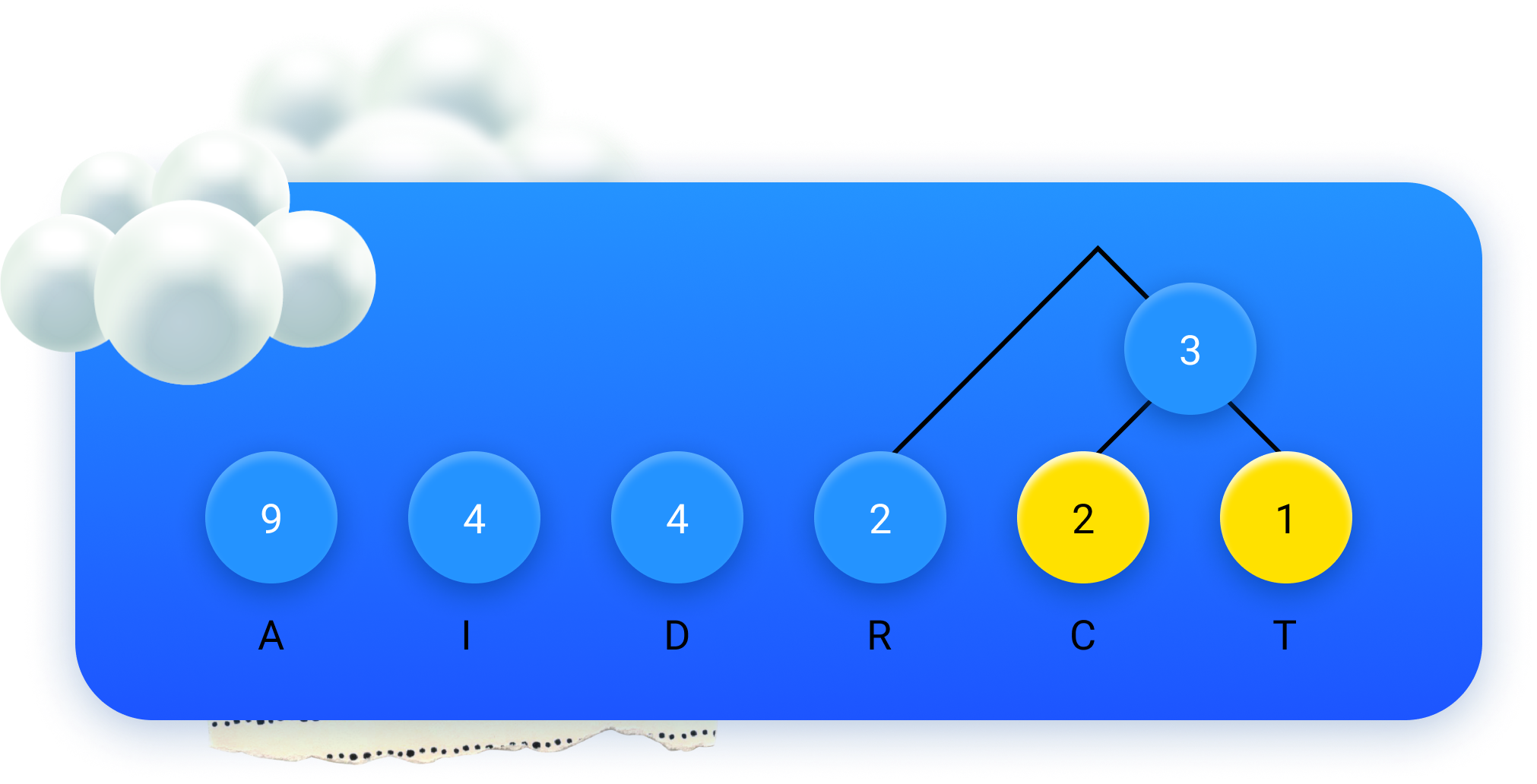
...pintamo-los de amarelo...
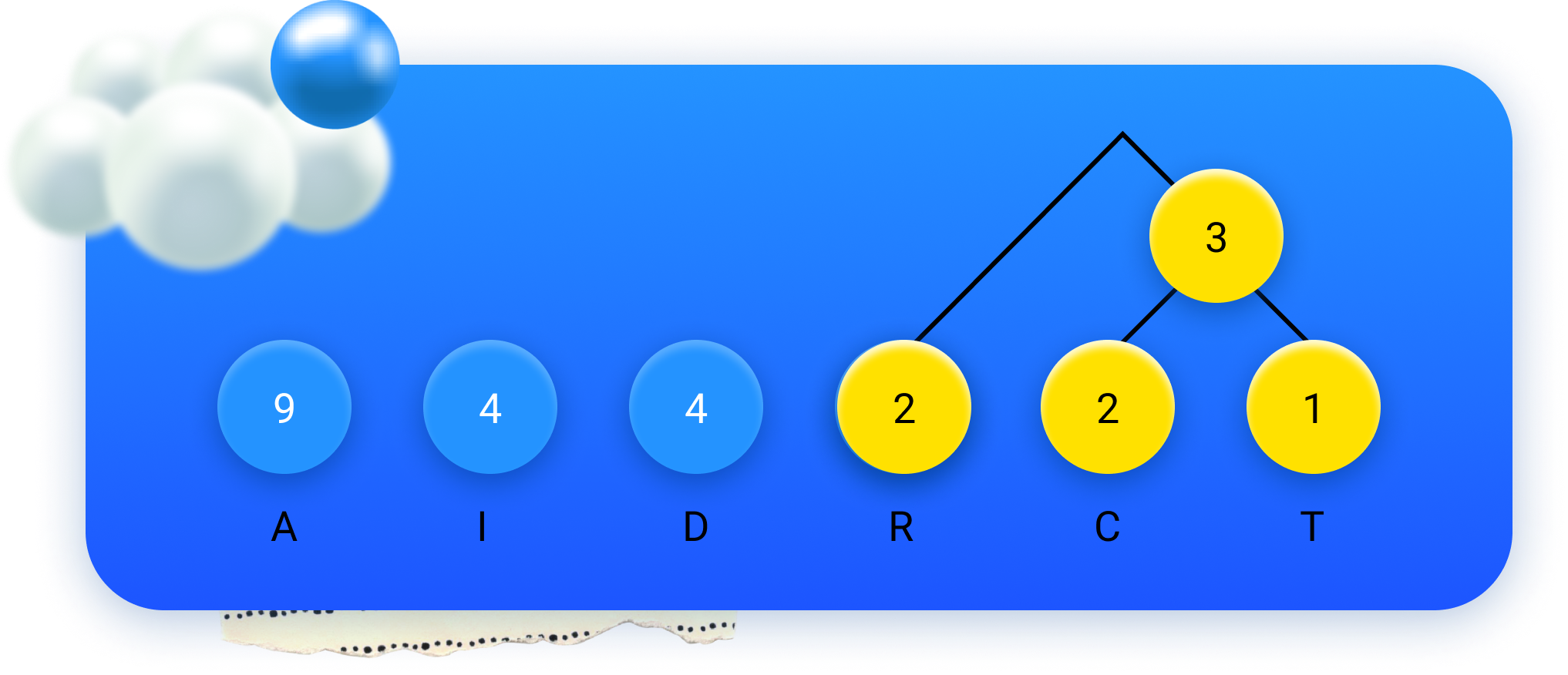
...e desenhamos um círculo a azul com a sua soma:
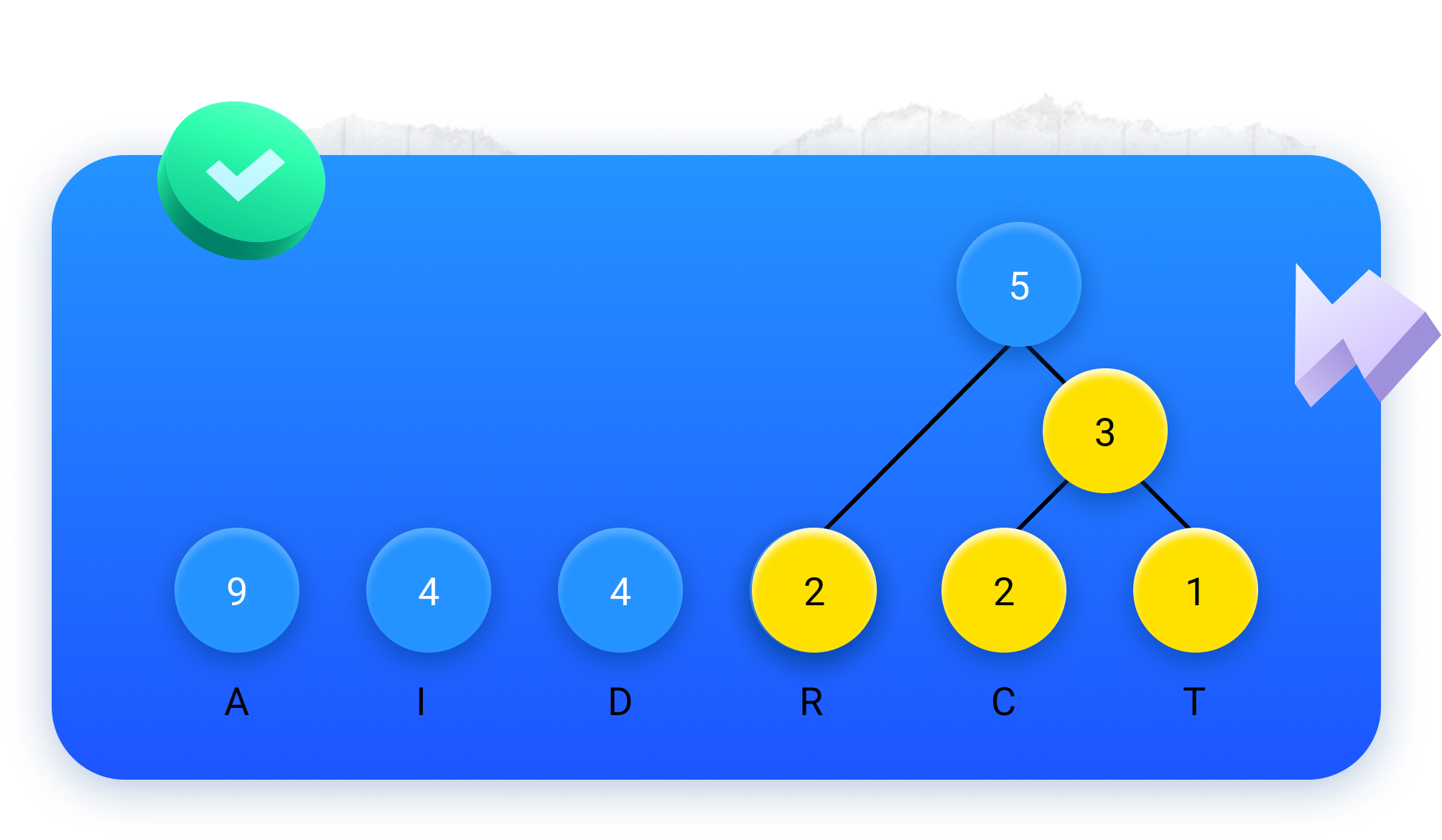
Repetindo estes passos mais algumas vezes, obtemos o seguinte diagrama:
Agora, por cima de cada “ramo” que vira para a direita, colocamos um 1; por cima de cada “ramo” que vira para a esquerda, colocamos um 0.
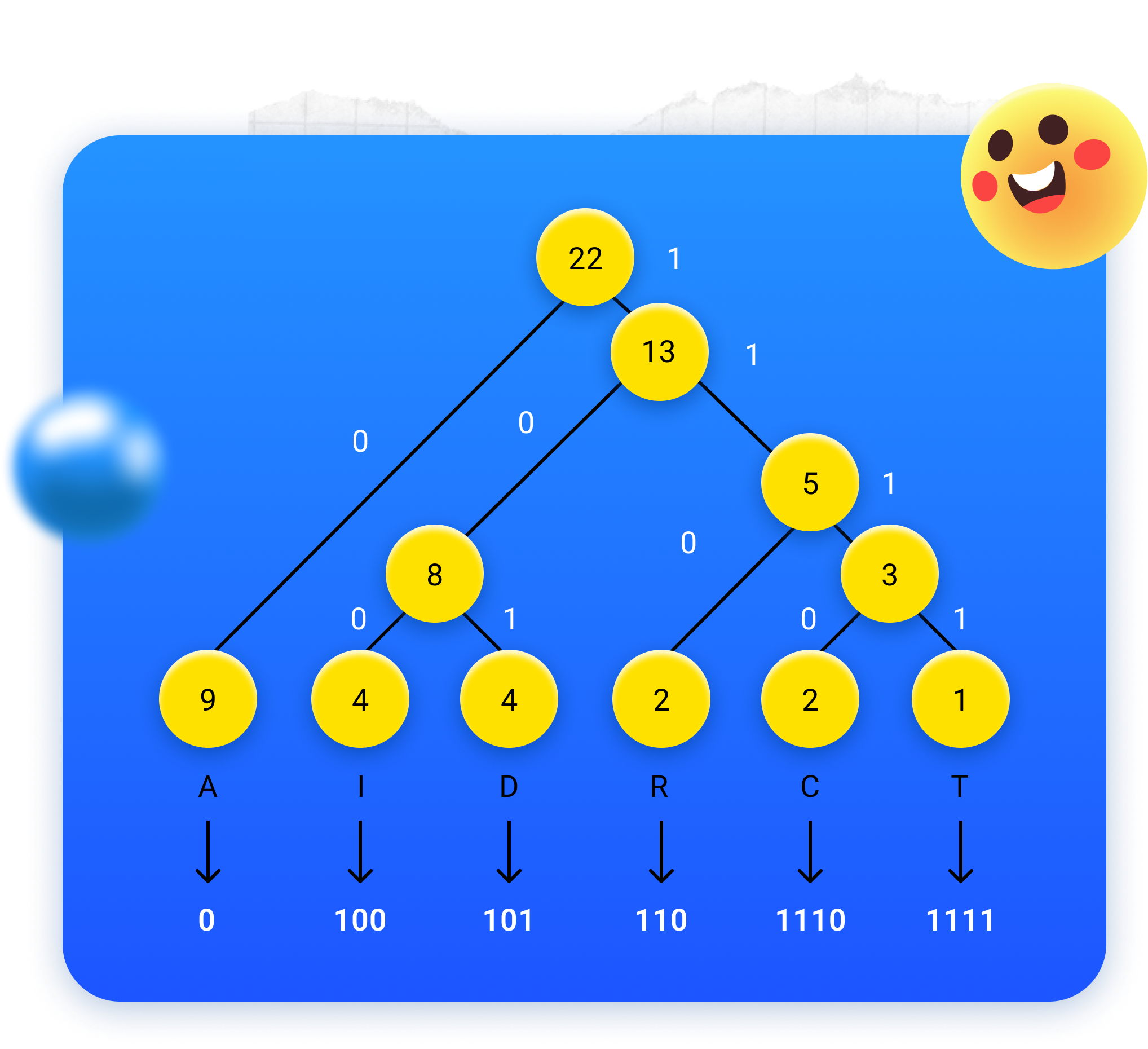
Se leres os códigos binários das letras percorrendo a árvore como já te ensinamos, concluis que a codificação é a seguinte:
Assim, a mensagem “ACADADIAATIADACRIADARI” é convertida no código binário

Trata-se de uma sequência com 51 bits, o que significa que a mensagem já só vai custar 51€. Continua a ser cara, mas fica por menos de um terço do preço da codificação ASCII 😄
Repara que a atribuição de códigos de Huffman depende do texto que se quer codificar, uma vez que depende da frequência dos caracteres que nele surgem. A ideia deste algoritmo é atribuir códigos mais curtos a letras mais frequentes. Faz sentido, certo? Além disso, dado um texto qualquer, os códigos de Huffman minimizam o comprimento médio das sequências de bits utilizadas para representar cada caracter. Nesse aspeto, uma compressão melhor é impossível. Os códigos de Huffman são mesmo um espetáculo! 😎

Imagina que és um detetive e queres comunicar que aconteceu um assassinato. No entanto, só podes transmitir uma mensagem através de sinais luminosos, sendo que uma emissão de luz é interpretada como um “1” e a ausência de luz é interpretada como um “0”.
Utiliza a codificação de Huffman para representar a mensagem “ASSASSINAR” através de uma sequência de 0s e 1s, de forma a conseguires comunicar de forma eficiente utilizando uma lanterna.
Resolução do desafio de "Computadores a "Cores""
1. Conseguimos representar 256 × 256 × 256 = 16 777 216 cores distintas.
2. É o código (143, 25, 192).
Colaboração de Mano a Mano Graphic Design Club
[Às quintas-feiras, o PÚBLICO na Escola dá espaço às ciências da computação, numa parceria com a ENSICO - Associação para o Ensino da Computação.]
O crescimento explosivo da geração e consumo de dados no mundo digital obriga as organizações a terem necessidade de usar técnicas eficientes para armazenar e transmitir dados. Como os recursos são limitados, as técnicas de compressão de dados são a via para minimizar o tamanho dos dados armazenados ou comunicados. Os recentes avanços no campo das tecnologias de informação resultaram na geração de uma enorme quantidade de dados a cada segundo, um desafio para os media, como nos explica o editor de fotografia do PÚBLICO, Miguel Manso.
Gerir notificações
Estes são os autores e tópicos que escolheu seguir. Pode activar ou desactivar as notificações.
Gerir notificações
Receba notificações quando publicamos um texto deste autor ou sobre os temas deste artigo.
Estes são os autores e tópicos que escolheu seguir. Pode activar ou desactivar as notificações.
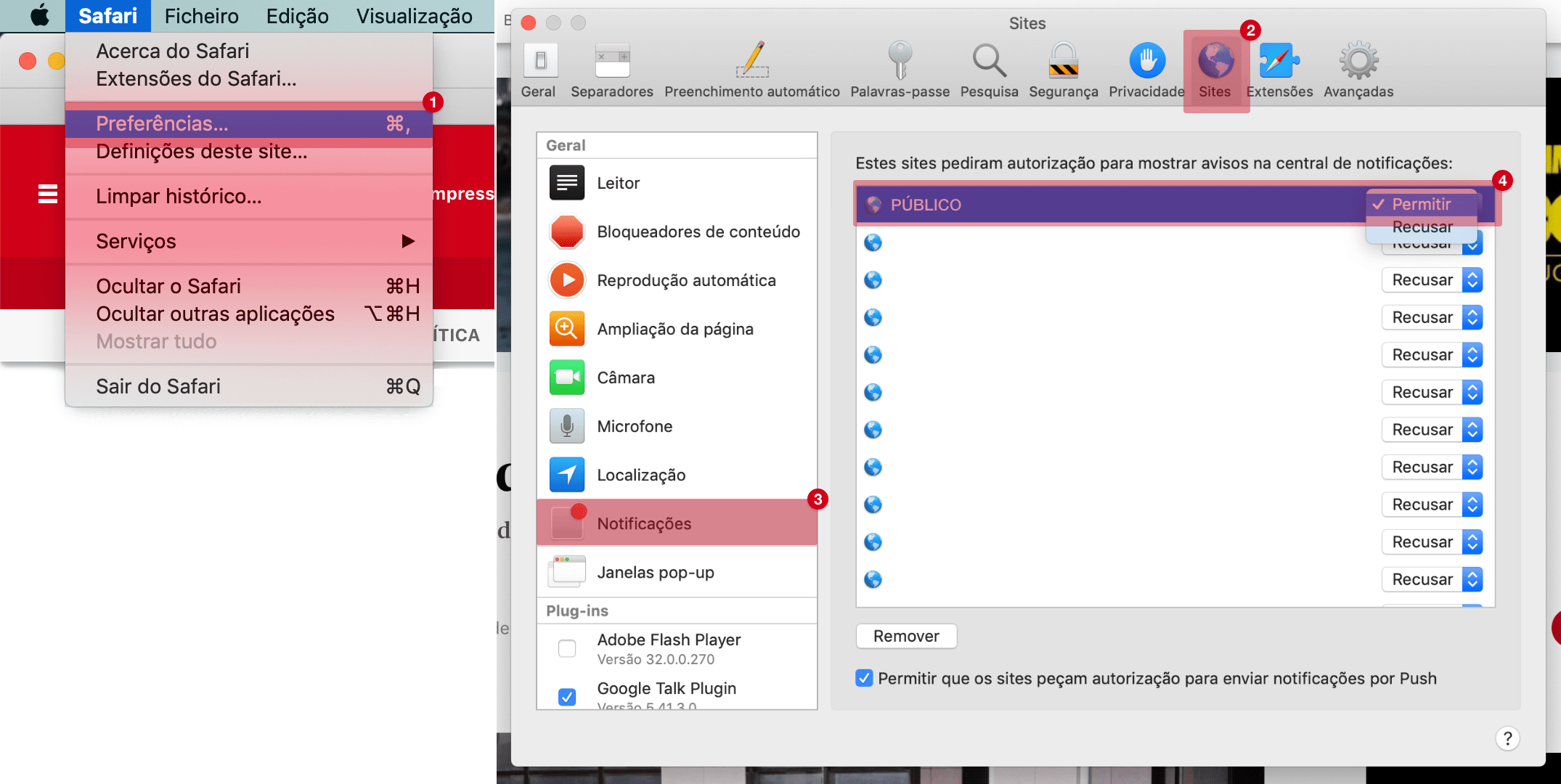
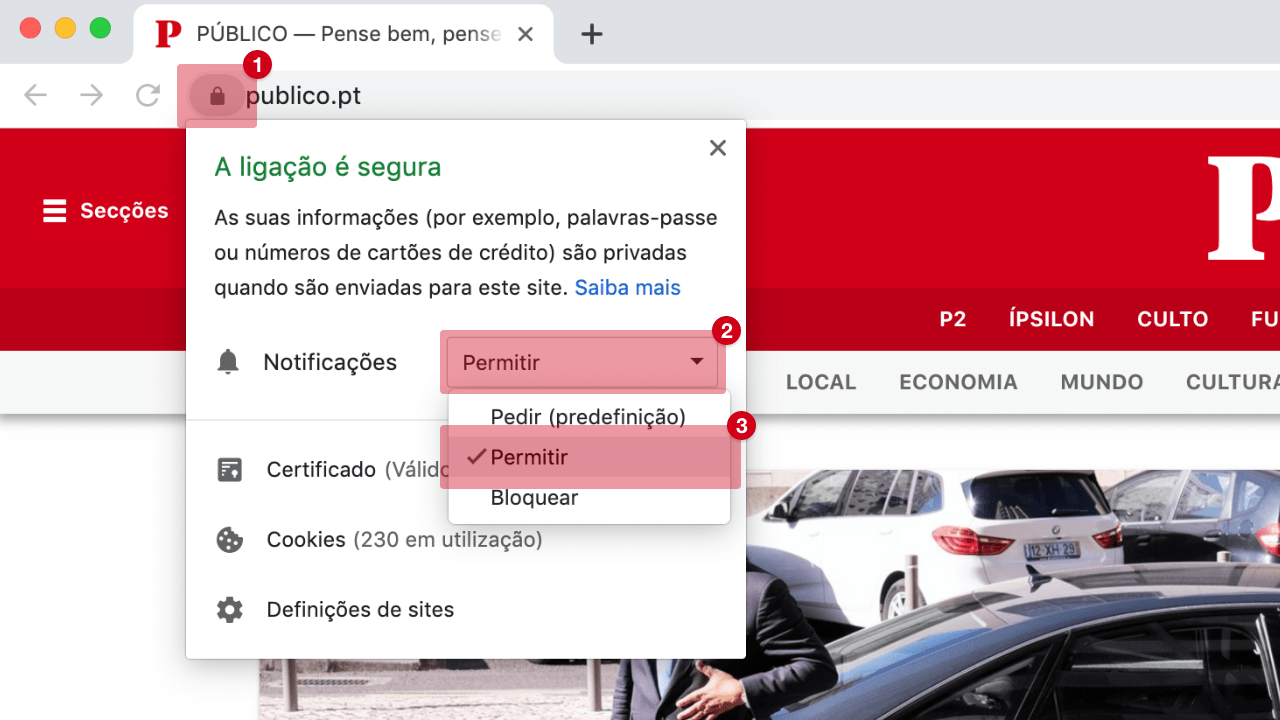
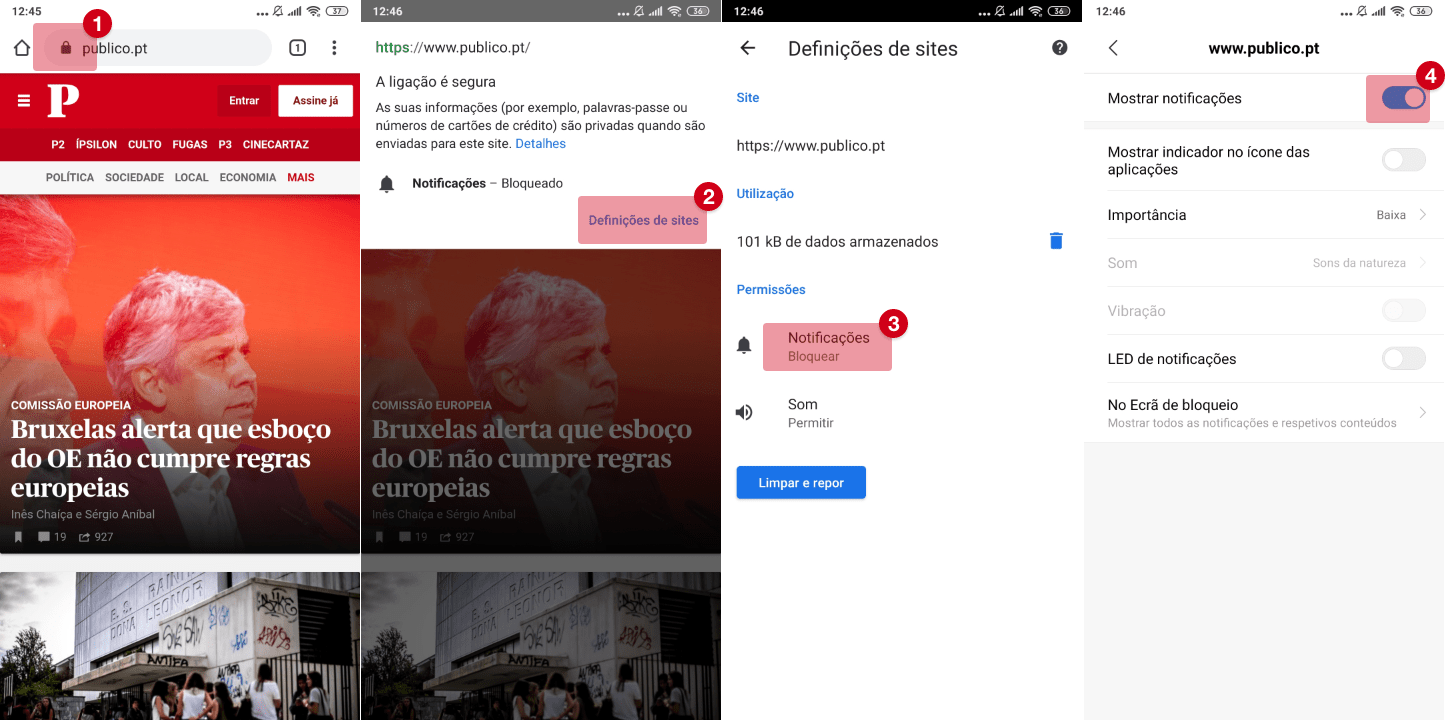
Notificações bloqueadas
Para permitir notificações, siga as instruções: